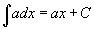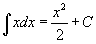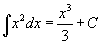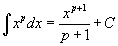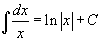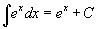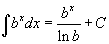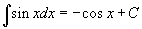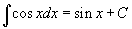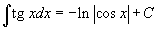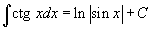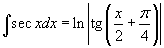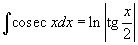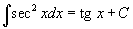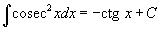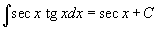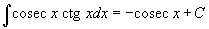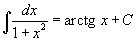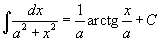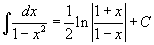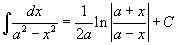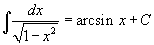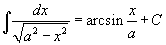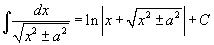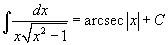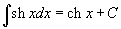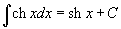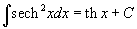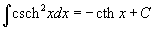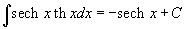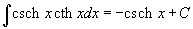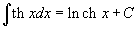Если существует предел

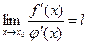, то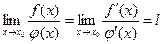

Применим к функциям f(x) и φ(x) теорему Коши для отрезка [x₀;x], лежащего в окрестности точки x₀, тогда

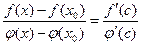, где с лежит между x₀ и х.

При x→x₀ величина с также стремится к х₀; перейдем в предыдущем равенстве к пределу:

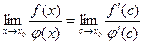
Так как 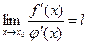, то .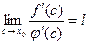

Поэтому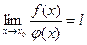

(предел отношения двух бесконечно малых равен пределу отношения их производных, если последний существует)

Правило Лопиталя, при ∞ / ∞.

Пусть функции f(x) и φ(x) непрерывны и дифференцируемы в окрестности точки x₀ (кроме точки x₀), в этой окрестности

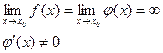
15.

Если у=f(x) непрерывна на [a,b] и дифференцируема на этом отрезке, то у=f(x)-const, тогда и только тогда, когда f¢(x)=0 при "х'[a,b]. Если функция непрерывна, дифференцируема на (a,b) и внутри (a,b) сохраняет знак, то функция у=f(x) монотонна.

16. Достаточное условие существования экстремума. Пусть функция f(x,y) имеет непрерывные частные производные второго порядка в некоторой окрестности стационарной точки М₀(x₀,y₀). Положим D= f¢¢_xx(M₀)f¢¢_yy(M₀) – (f¢¢_xy(M₀)². тогда:

1. если D>0, то в точке М₀ функция имеет локальный экстремум, причём f¢¢_xx(M₀)<0 – локальный максимум, при f¢¢_xx(M₀)>0 – локальный минимум;
2. если D<0, то в точке М₀ нет экстремума.
3. если D=0, то требуются дополнительные исследования.

17.

График ф-ии яв-ся выпуклым на некот промеж, если все его точки леж. ниже люб касат, провед к этой кривой. Вогнутый - наоборот. выпуклости (f''(x)<0), вогнутости (f''(x)>0)

Точка перегиба – точка, отделяющ выпук часть непрер прямой от вогнутой части.

Необходимое условие - чтобы f”(x₁)=0

Достаточное условие - смена знака второй производной при переходе через эту точку.

18.. Асимптотой

графика ф-ии y=f(x) называется прямая, обладающая тем свойством, что расстояние от точки (х, f(x)) до этой прямой стремится к 0 при неограниченном удалении точки графика от начала координат.

Если для некоторого х0 имеет место предел f(x)=∞ при х→х0 то говорят, что х=х0 явл. вертикальн. асимптотой f(x). Вертикальные асимптоты следует искать в точках разрыва ф-ии или на концах её ООФ (а;в) если а и в конечные числа Если предел f(x)=b при x→∞ то говорят, что у=b явл. горизонтальной асимптотой f(x) Если предел f(x)/х=k при x→∞ (k≠0;k≠∞) и предел (f(x)-kx)=b, то y=kx+b является наклонной асимпт-й

Наклонная асимптота как и горизонтальная может быть правосторонней или левосторонней

1 ООФ, ОЗФ 2 Непрерывность ф-ии 3 Нахождение асимптот 4 Экстремумы и интервалы монотонности

5 Интервалы выпуклости и т. перегиба 6 Чётность нечётность, периодичность 7 Т. пересечения с Ох и Оу

Неопределенный интеграл и его свойства. Таблица интегралов.

Определение первообразной и неопределенного интеграла Функция F (x) называется первообразной функции f (x), если 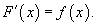Множество всех первообразных некоторой функции f (x) называется неопределенным интегралом функции f (x) и обозначается как 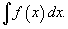Таким образом, если F - некоторая частная первообразная, то справедливо выражение 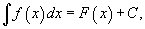где С - произвольная постоянная. 20.Свойства неопределенного интеграла В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f, а, k, C - постоянные величины. · 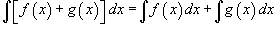· · 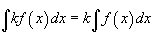· 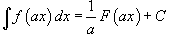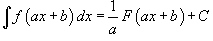Таблица интегралов В формулах ниже предполагается, что a, p (p ≠ 1), C - действительные постоянные, b - основание показательной функции (b ≠ 1, b > 0).

21.

-Непосредственное интегрирование

Метод интегрирования, при котором интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием. См. Таблица интегралов.

[править]Подведение под знак дифференциала

Данный метод эквивалентен методу замены переменной (см. далее):

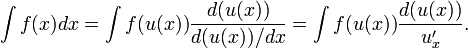
[править]Метод замены переменной (метод подстановки)

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.

Пусть требуется вычислить интеграл 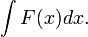Сделаем подстановку 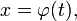где 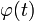— функция, имеющая непрерывную производную.

Тогда 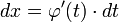и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:

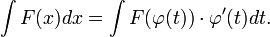
[править]Интегрирование выражений вида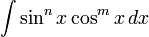

Если m нечётное, m > 0, то удобнее сделать подстановку sin x = t.

Если n нечётное, n > 0, то удобнее сделать подстановку cos x = t.

Если n и m чётные, то удобнее сделать подстановку tg x = t.

[править]Примеры

Вычислить: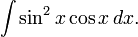

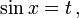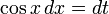Пусть тогда и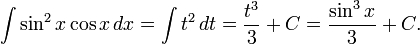

[править]Интегрирование по частям

Основная статья: Интегрирование по частям

Интегрирование по частям — применение следующей формулы для интегрирования:

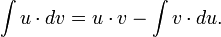
В частности, с помощью n -кратного применения этой формулы находится интеграл

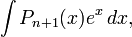
где 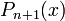— многочлен 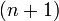-ой степени.

[править]Интегрирование рациональных дробей

Основная статья: Разложение дробей при интегрировании

Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором знаменатель дроби не обращается в ноль, существует и выражается через элементарные функции, а именно он является алгебраической суммой суперпозиции рациональных дробей, арктангенсов и рациональных логарифмов.

Сам метод заключается в разложении рациональной дроби на сумму простейших дробей.

Всякую правильную рациональную дробь 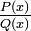, знаменатель которой разложен на множители

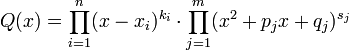
можно представить (и притом единственным образом) в виде следующей суммы простейших дробей:

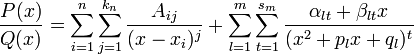
где 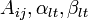— некоторые действительные коэффициенты, обычно вычисляемые с помощью метода неопределённых коэффициентов.

[править]Примеры

Вычислить: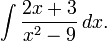

Разложим подынтегральное выражение на простейшие дроби:

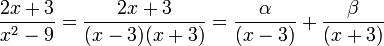
Сгруппируем слагаемые и приравняем коэффициенты при членах с одинаковыми степенями:

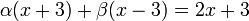
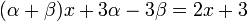
Следовательно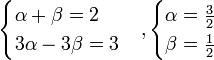

Тогда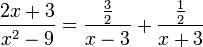

Теперь легко вычислить исходный интеграл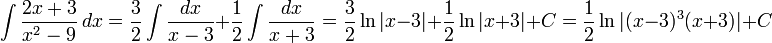

22. [править]Интегрирование по частям

Основная статья: Интегрирование по частям

Интегрирование по частям — применение следующей формулы для интегрирования:

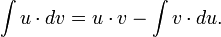
В частности, с помощью n -кратного применения этой формулы находится интеграл

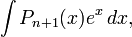
где 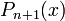— многочлен 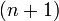-ой степени.

Дата добавления: 2015-04-24