Понятие определенного интеграла

Интегралы от некоторых трансцендентных функций

К этому виду относятся, например, интегралы:

, ,

, ,

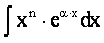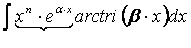, (n - целое).

Все интегралы такого типа вычисляются, вообще говоря, с помощью интегрирования по частям (повторного интегрирования по частям).

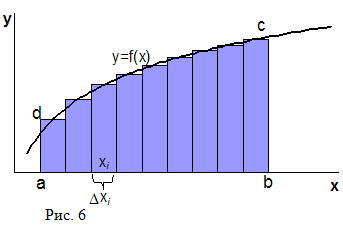К понятию определенного интеграла приходят при решении задач о вычислении площади под графиком какой-либо функции. Приближенно площадь фигуры abcd на рис. 6 может быть посчитана как сумма площадей n прямоугольников, на которые мы её разбили: Предел интегральной суммы при 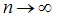называется определенным интегралом от функции f(x) на промежутке [a,b]: При этом а называется нижним пределом, а b - верхним пределом определенного интеграла. Геометрический смысл определенного интеграла: он равен площади криволинейной трапеции, ограниченной прямыми x = a, x = b, y = 0 и y = f(x). Если функция проходит под осью x, то перед площадью ставится знак «-». Например, в физике определенный интеграл применяется для расчета работы А, произведенной силой c проекцией на ось x, равной F(x), при перемещении точки приложения силы вдоль оси x от точки а до точки b:  

28. Основные свойства интеграла. Установим ряд важных свойств определенного интеграла. Большая часть этих свойств присуща интегралам от любых интегрируемых функций, но мы будем формулировать их для функций непрерывных.

Теорема 1. Если f (x) и g (x) - две непрерывные функции, заданные на промежутке [ a, b ], то

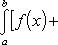
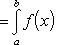
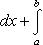
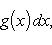
т. е. интеграл суммы равен сумме интегралов слагаемых.

В самом деле, составляя интегральную сумму для функции f (x) + g (x), очевидно, будем иметь

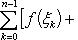
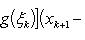
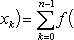
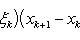
после чего остается перейти к пределу при λ → 0.

Аналогично доказывается

Теорема 2. Если f (x) - непрерывная функция, а c - постоянное число, то

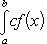
т. е. постоянный множитель можно выносить за знак интеграла.

Теорема 3. Пусть f (x) непрерывна на промежутке [ a, b ]. Если этот промежуток точкой c разложен на части [ a, c ] и [ c, b ], то интеграл по всему промежутку оказывается равным сумме интегралов по его частям, т. е.

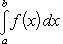
В самом деле, будем при раздроблении промежутка [ a, b ] на части включать c в число точек деления. Если c = x_m, то

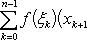
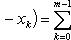
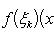
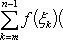
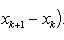
Каждая из написанных здесь трех сумм является интегральной суммой соответственно для промежутков [ a, b ], [ a, c ] и [ c, b ]. Остается перейти к пределу при λ → 0.

Дата добавления: 2015-04-24