
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример. Приводя к общему знаменателю и приравнивая соответствующие числители, получаем:
|
|
|
|
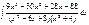
Т.к. (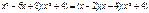 , то
, то

Приводя к общему знаменателю и приравнивая соответствующие числители, получаем:
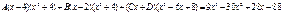
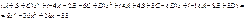

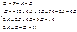





Итого:
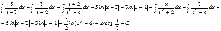
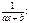 III.
III. 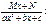 II.
II. 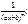 IV.
IV. 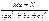 m, n – натуральные числа (m ³ 2, n ³ 2) и b2 – 4ac <0.
Первые два типа интегралов от элементарных дробей довольно просто приводятся к табличным подстановкой t = ax + b.
I.
m, n – натуральные числа (m ³ 2, n ³ 2) и b2 – 4ac <0.
Первые два типа интегралов от элементарных дробей довольно просто приводятся к табличным подстановкой t = ax + b.
I.  II.
II. 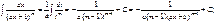 Рассмотрим метод интегрирования элементарных дробей вида III.
Интеграл дроби вида III может быть представлен в виде:
Рассмотрим метод интегрирования элементарных дробей вида III.
Интеграл дроби вида III может быть представлен в виде:
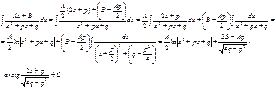 Здесь в общем виде показано приведение интеграла дроби вида III к двум табличным интегралам.
Рассмотрим применение указанной выше формулы на примерах.
Пример.
Здесь в общем виде показано приведение интеграла дроби вида III к двум табличным интегралам.
Рассмотрим применение указанной выше формулы на примерах.
Пример.
 Вообще говоря, если у трехчлена ax2 + bx + c выражение b2 – 4ac >0, то дробь по определению не является элементарной, однако, тем не менее ее можно интегрировать указанным выше способом.
Пример.
Вообще говоря, если у трехчлена ax2 + bx + c выражение b2 – 4ac >0, то дробь по определению не является элементарной, однако, тем не менее ее можно интегрировать указанным выше способом.
Пример.
 Пример.
Пример.
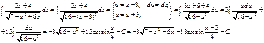 Рассмотрим теперь методы интегрирования простейших дробей IV типа.
Сначала рассмотрим частный случай при М = 0, N = 1.
Тогда интеграл вида
Рассмотрим теперь методы интегрирования простейших дробей IV типа.
Сначала рассмотрим частный случай при М = 0, N = 1.
Тогда интеграл вида  можно путем выделения в знаменателе полного квадрата представить в виде
можно путем выделения в знаменателе полного квадрата представить в виде 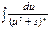 . Сделаем следующее преобразование:
. Сделаем следующее преобразование:
 .Второй интеграл, входящий в это равенство, будем брать по частям.
Обозначим:
.Второй интеграл, входящий в это равенство, будем брать по частям.
Обозначим: 
 Для исходного интеграла получаем:
Для исходного интеграла получаем:

 Полученная формула называется рекуррентной. Если применить ее n-1 раз, то получится табличный интеграл
Полученная формула называется рекуррентной. Если применить ее n-1 раз, то получится табличный интеграл 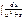 .
Вернемся теперь к интегралу от элементарной дроби вида IV в общем случае.
.
Вернемся теперь к интегралу от элементарной дроби вида IV в общем случае.
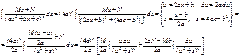 В полученном равенстве первый интеграл с помощью подстановки t = u2 + s приводится к табличному
В полученном равенстве первый интеграл с помощью подстановки t = u2 + s приводится к табличному  , а ко второму интегралу применяется рассмотренная выше рекуррентная формула.
Несмотря на кажущуюся сложность интегрирования элементарной дроби вида IV, на практике его достаточно легко применять для дробей с небольшой степенью n, а универсальность и общность подхода делает возможным очень простую реализацию этого метода на ЭВМ.
, а ко второму интегралу применяется рассмотренная выше рекуррентная формула.
Несмотря на кажущуюся сложность интегрирования элементарной дроби вида IV, на практике его достаточно легко применять для дробей с небольшой степенью n, а универсальность и общность подхода делает возможным очень простую реализацию этого метода на ЭВМ.
 Билет №29
Логарифмическое дифференцирование.
Рассмотрим функцию
Билет №29
Логарифмическое дифференцирование.
Рассмотрим функцию  .
Тогда (lnïxï)¢=
.
Тогда (lnïxï)¢= 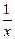 , т.к.
, т.к. 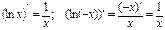 .
Учитывая полученный результат, можно записать
.
Учитывая полученный результат, можно записать 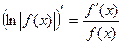 .
Отношение
.
Отношение 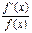 называется логарифмической производной функции f(x).
Способ логарифмического дифференцированиясостоит в том, что сначала находят логарифмическую производную функции, а затем производную самой функции по формуле
называется логарифмической производной функции f(x).
Способ логарифмического дифференцированиясостоит в том, что сначала находят логарифмическую производную функции, а затем производную самой функции по формуле
 Способ логарифмического дифференцирования удобно применять для нахождения производных сложных, особенно показательных функций, для которых непосредственное вычисление производной с использованием правил дифференцирования представляется трудоемким.
Производная показательно- степенной функции.
Функция называется показательной, если независимая переменная входит в показатель степени, и степенной, если переменная является основанием. Если же и основание и показатель степени зависят от переменной, то такая функция будет показательно – степенной.
Пусть u = f(x) и v = g(x) – функции, имеющие производные в точке х, f(x)>0.
Найдем производную функции y = uv. Логарифмируя, получим:
lny = vlnu
Способ логарифмического дифференцирования удобно применять для нахождения производных сложных, особенно показательных функций, для которых непосредственное вычисление производной с использованием правил дифференцирования представляется трудоемким.
Производная показательно- степенной функции.
Функция называется показательной, если независимая переменная входит в показатель степени, и степенной, если переменная является основанием. Если же и основание и показатель степени зависят от переменной, то такая функция будет показательно – степенной.
Пусть u = f(x) и v = g(x) – функции, имеющие производные в точке х, f(x)>0.
Найдем производную функции y = uv. Логарифмируя, получим:
lny = vlnu
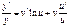

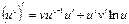 Пример. Найти производную функции
Пример. Найти производную функции  .
По полученной выше формуле получаем:
.
По полученной выше формуле получаем:  Производные этих функций:
Производные этих функций:  Окончательно:
Окончательно:

 .
Здесь R – обозначение некоторой рациональной функции от переменных sinx и cosx.
Интегралы этого вида вычисляются с помощью подстановки
.
Здесь R – обозначение некоторой рациональной функции от переменных sinx и cosx.
Интегралы этого вида вычисляются с помощью подстановки  . Эта подстановка позволяет преобразовать тригонометрическую функцию в рациональную.
. Эта подстановка позволяет преобразовать тригонометрическую функцию в рациональную.
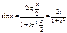 ,
, 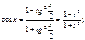 Тогда
Тогда 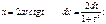 Таким образом:
Таким образом: 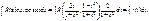 Описанное выше преобразование называется универсальной тригонометрической подстановкой.
Пример.
Описанное выше преобразование называется универсальной тригонометрической подстановкой.
Пример.
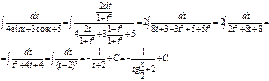 Несомненным достоинством этой подстановки является то, что с ее помощью всегда можно преобразовать тригонометрическую функцию в рациональную и вычислить соответствующий интеграл. К недостаткам можно отнести то, что при преобразовании может получиться достаточно сложная рациональная функция, интегрирование которой займет много времени и сил.
Однако при невозможности применить более рациональную замену переменной этот метод является единственно результативным.
Пример.
Несомненным достоинством этой подстановки является то, что с ее помощью всегда можно преобразовать тригонометрическую функцию в рациональную и вычислить соответствующий интеграл. К недостаткам можно отнести то, что при преобразовании может получиться достаточно сложная рациональная функция, интегрирование которой займет много времени и сил.
Однако при невозможности применить более рациональную замену переменной этот метод является единственно результативным.
Пример.
 Интеграл вида
Интеграл вида 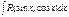 если
функция R является нечетной относительно cosx.
Несмотря на возможность вычисления такого интеграла с помощью универсальной тригонометрической подстановки, рациональнее применить подстановку t = sinx.
если
функция R является нечетной относительно cosx.
Несмотря на возможность вычисления такого интеграла с помощью универсальной тригонометрической подстановки, рациональнее применить подстановку t = sinx.
 Функция
Функция  может содержать cosx только в четных степенях, а следовательно, может быть преобразована в рациональную функцию относительно sinx.
может содержать cosx только в четных степенях, а следовательно, может быть преобразована в рациональную функцию относительно sinx.
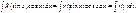 Пример.
Пример.
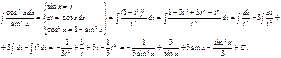 Вообще говоря, для применения этого метода необходима только нечетность функции относительно косинуса, а степень синуса, входящего в функцию может быть любой, как целой, так и дробной.
Вообще говоря, для применения этого метода необходима только нечетность функции относительно косинуса, а степень синуса, входящего в функцию может быть любой, как целой, так и дробной.
 где n- натуральное число.
С помощью подстановки
где n- натуральное число.
С помощью подстановки 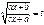 функция рационализируется.
функция рационализируется.
 Тогда
Тогда 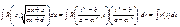 Пример.
Пример.

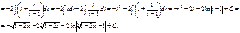 Если в состав иррациональной функции входят корни различных степеней, то в качестве новой переменной рационально взять корень степени, равной наименьшему общему кратному степеней корней, входящих в выражение.
Проиллюстрируем это на примере.
Пример.
Если в состав иррациональной функции входят корни различных степеней, то в качестве новой переменной рационально взять корень степени, равной наименьшему общему кратному степеней корней, входящих в выражение.
Проиллюстрируем это на примере.
Пример.
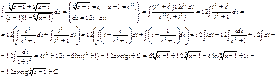 Интегрирование биноминальных дифференциалов.
Определение: Биноминальным дифференциаломназывается выражение
xm(a + bxn)pdx
где m, n, и p – рациональные числа.
Как было доказано академиком Чебышевым П.Л. (1821-1894), интеграл от биноминального дифференциала может быть выражен через элементарные функции только в следующих трех случаях:
1) Если р – целое число, то интеграл рационализируется с помощью подстановки
Интегрирование биноминальных дифференциалов.
Определение: Биноминальным дифференциаломназывается выражение
xm(a + bxn)pdx
где m, n, и p – рациональные числа.
Как было доказано академиком Чебышевым П.Л. (1821-1894), интеграл от биноминального дифференциала может быть выражен через элементарные функции только в следующих трех случаях:
1) Если р – целое число, то интеграл рационализируется с помощью подстановки
 , где l - общий знаменатель m и n.
2) Если
, где l - общий знаменатель m и n.
2) Если  - целое число, то интеграл рационализируется подстановкой
- целое число, то интеграл рационализируется подстановкой
 , где s – знаменатель числа р.
3) Если
, где s – знаменатель числа р.
3) Если  - целое число, то используется подстановка
- целое число, то используется подстановка  , где s – знаменатель числа р.
Однако, наибольшее практическое значение имеют интегралы от функций, рациональных относительно аргумента и квадратного корня из квадратного трехчлена.
На рассмотрении этих интегралов остановимся более подробно.
Интегралы вида
, где s – знаменатель числа р.
Однако, наибольшее практическое значение имеют интегралы от функций, рациональных относительно аргумента и квадратного корня из квадратного трехчлена.
На рассмотрении этих интегралов остановимся более подробно.
Интегралы вида  .
Существует несколько способов интегрирования такого рода функций. В зависимости от вида выражения, стоящего под знаком радикала, предпочтительно применять тот или иной способ.
Как известно, квадратный трехчлен путем выделения полного квадрата может быть приведен к виду:
.
Существует несколько способов интегрирования такого рода функций. В зависимости от вида выражения, стоящего под знаком радикала, предпочтительно применять тот или иной способ.
Как известно, квадратный трехчлен путем выделения полного квадрата может быть приведен к виду:
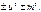 Таким образом, интеграл приводится к одному из трех типов:
1)
Таким образом, интеграл приводится к одному из трех типов:
1) 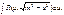 2)
2) 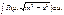
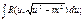 2 способ. Подстановки Эйлера.(1707-1783)
1) Если а>0, то интеграл вида
2 способ. Подстановки Эйлера.(1707-1783)
1) Если а>0, то интеграл вида 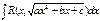 рационализируется подстановкой
рационализируется подстановкой
 .
2) Если a<0 и c>0, то интеграл вида
.
2) Если a<0 и c>0, то интеграл вида 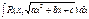 рационализируется подстановкой
рационализируется подстановкой  .
3) Если a<0, а подкоренное выражение раскладывается на действительные множители a(x – x1)(x – x2), то интеграл вида
.
3) Если a<0, а подкоренное выражение раскладывается на действительные множители a(x – x1)(x – x2), то интеграл вида 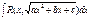 рационализируется подстановкой
рационализируется подстановкой 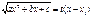 .
Отметим, что подстановки Эйлера неудобны для практического использования,
т.к. даже при несложных подинтегральных функциях приводят к весьма громоздким вычислениям. Эти подстановки представляют скорее теоретический интерес.
Билет№42
Вычисление определенного интеграла.
Пусть в интеграле
.
Отметим, что подстановки Эйлера неудобны для практического использования,
т.к. даже при несложных подинтегральных функциях приводят к весьма громоздким вычислениям. Эти подстановки представляют скорее теоретический интерес.
Билет№42
Вычисление определенного интеграла.
Пусть в интеграле 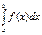 нижний предел а = const, а верхний предел b изменяется. Очевидно, что если изменяется верхний предел, то изменяется и значение интеграла.
Обозначим
нижний предел а = const, а верхний предел b изменяется. Очевидно, что если изменяется верхний предел, то изменяется и значение интеграла.
Обозначим  = Ф(х). Найдем производную функции Ф(х) по переменному верхнему пределу х.
= Ф(х). Найдем производную функции Ф(х) по переменному верхнему пределу х.
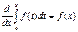 Аналогичную теорему можно доказать для случая переменного нижнего предела.
Теорема: Для всякой функции f(x), непрерывной на отрезке [a, b], существует на этом отрезке первообразная, а значит, существует неопределенный интеграл.
Теорема: (Теорема Ньютона – Лейбница)
Если функция F(x) – какая- либо первообразная от непрерывной функции f(x), то
Аналогичную теорему можно доказать для случая переменного нижнего предела.
Теорема: Для всякой функции f(x), непрерывной на отрезке [a, b], существует на этом отрезке первообразная, а значит, существует неопределенный интеграл.
Теорема: (Теорема Ньютона – Лейбница)
Если функция F(x) – какая- либо первообразная от непрерывной функции f(x), то
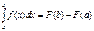 это выражение известно под названием формулы Ньютона – Лейбница.
Доказательство: Пусть F(x) – первообразная функции f(x). Тогда в соответствии с приведенной выше теоремой, функция
это выражение известно под названием формулы Ньютона – Лейбница.
Доказательство: Пусть F(x) – первообразная функции f(x). Тогда в соответствии с приведенной выше теоремой, функция  - первообразная функция от f(x). Но т.к. функция может иметь бесконечно много первообразных, которые будут отличаться друг от друга только на какое – то постоянное число С, то
- первообразная функция от f(x). Но т.к. функция может иметь бесконечно много первообразных, которые будут отличаться друг от друга только на какое – то постоянное число С, то
 при соответствующем выборе С это равенство справедливо для любого х, т.е. при х = а:
при соответствующем выборе С это равенство справедливо для любого х, т.е. при х = а:

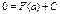
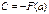 Тогда
Тогда 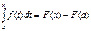 .
А при х = b:
.
А при х = b: 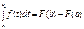 Заменив переменную t на переменную х, получаем формулу Ньютона – Лейбница:
Заменив переменную t на переменную х, получаем формулу Ньютона – Лейбница:
 Теорема доказана.
Иногда применяют обозначение F(b) – F(a) = F(x)
Теорема доказана.
Иногда применяют обозначение F(b) – F(a) = F(x) 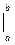 .
Формула Ньютона – Лейбница представляет собой общий подход к нахождению определенных интегралов.
Что касается приемов вычисления определенных интегралов, то они практически ничем не отличаются от всех тех приемов и методов, которые были рассмотрены выше при нахождении неопределенных интегралов.
Точно так же применяются методы подстановки (замены переменной), метод интегрирования по частям, те же приемы нахождения первообразных для тригонометрических, иррациональных и трансцендентных функций. Особенностью является только то, что при применении этих приемов надо распространять преобразование не только на подинтегральную функцию, но и на пределы интегрирования. Заменяя переменную интегрирования, не забыть изменить соответственно пределы интегрирования.
.
Формула Ньютона – Лейбница представляет собой общий подход к нахождению определенных интегралов.
Что касается приемов вычисления определенных интегралов, то они практически ничем не отличаются от всех тех приемов и методов, которые были рассмотрены выше при нахождении неопределенных интегралов.
Точно так же применяются методы подстановки (замены переменной), метод интегрирования по частям, те же приемы нахождения первообразных для тригонометрических, иррациональных и трансцендентных функций. Особенностью является только то, что при применении этих приемов надо распространять преобразование не только на подинтегральную функцию, но и на пределы интегрирования. Заменяя переменную интегрирования, не забыть изменить соответственно пределы интегрирования.
 n = m1Dx1 + m2Dx2 + … +mnDxn =
n = m1Dx1 + m2Dx2 + … +mnDxn = 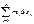
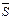 n = M1Dx1 + M2Dx2 + … + MnDxn =
n = M1Dx1 + M2Dx2 + … + MnDxn =  Сумма
Сумма  называется нижней интегральной суммой, а сумма
называется нижней интегральной суммой, а сумма 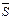 – верхней интегральной суммой.
Т.к. mi £ Mi, то
– верхней интегральной суммой.
Т.к. mi £ Mi, то 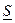 n £
n £  n, а m(b – a) £
n, а m(b – a) £ 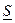 n £
n £  n £ M(b – a)
Внутри каждого отрезка выберем некоторую точку e.
x0 < e1 < x1, x1 < e < x2, …, xn-1 < e < xn.
Найдем значения функции в этих точках и составим выражение, которое называется интегральной суммой для функции f(x) на отрезке [a, b].
Sn = f(e1)Dx1 + f(e2)Dx2 + … + f(en)Dxn =
n £ M(b – a)
Внутри каждого отрезка выберем некоторую точку e.
x0 < e1 < x1, x1 < e < x2, …, xn-1 < e < xn.
Найдем значения функции в этих точках и составим выражение, которое называется интегральной суммой для функции f(x) на отрезке [a, b].
Sn = f(e1)Dx1 + f(e2)Dx2 + … + f(en)Dxn =  Тогда можно записать: miDxi £ f(ei)Dxi £ MiDxi
Следовательно,
Тогда можно записать: miDxi £ f(ei)Dxi £ MiDxi
Следовательно, 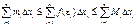
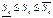 Геометрически это представляется следующим образом: график функции f(x) ограничен сверху описанной ломаной линией, а снизу – вписанной ломаной.
Обозначим maxDxi – наибольший отрезок разбиения, а minDxi – наименьший. Если maxDxi® 0, то число отрезков разбиения отрезка [a, b] стремится к бесконечности.
Если
Геометрически это представляется следующим образом: график функции f(x) ограничен сверху описанной ломаной линией, а снизу – вписанной ломаной.
Обозначим maxDxi – наибольший отрезок разбиения, а minDxi – наименьший. Если maxDxi® 0, то число отрезков разбиения отрезка [a, b] стремится к бесконечности.
Если 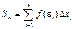 , то
, то 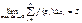 Определение: Если при любых разбиениях отрезка [a, b] таких, что maxDxi® 0 и произвольном выборе точек ei интегральная сумма
Определение: Если при любых разбиениях отрезка [a, b] таких, что maxDxi® 0 и произвольном выборе точек ei интегральная сумма  стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [a, b].
Обозначение:
стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [a, b].
Обозначение: 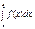 а – нижний предел, b – верхний предел, х – переменная интегрирования, [a, b] – отрезок интегрирования.
Определение: Если для функции f(x) существует предел
а – нижний предел, b – верхний предел, х – переменная интегрирования, [a, b] – отрезок интегрирования.
Определение: Если для функции f(x) существует предел 
 то функция называется интегрируемой на отрезке [a, b].
Также верны утверждения:
то функция называется интегрируемой на отрезке [a, b].
Также верны утверждения: 
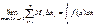 Теорема: Если функция f(x) непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.
Свойства определенного интеграла.
1)
Теорема: Если функция f(x) непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.
Свойства определенного интеграла.
1)  2)
2)  3)
3) 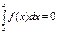 4) Если f(x) £ j(x) на отрезке [a, b] a < b, то
4) Если f(x) £ j(x) на отрезке [a, b] a < b, то 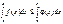 5) Если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b], то:
5) Если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b], то:
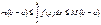 6) Теорема о среднем. Если функция f(x) непрерывна на отрезке [a, b], то на этом отрезке существует точка e такая, что
6) Теорема о среднем. Если функция f(x) непрерывна на отрезке [a, b], то на этом отрезке существует точка e такая, что
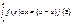 8)
8)  Билет№43
Замена переменных.
Пусть задан интеграл
Билет№43
Замена переменных.
Пусть задан интеграл  , где f(x) – непрерывная функция на отрезке [a, b].
Введем новую переменную в соответствии с формулой x = j(t).
Тогда если
1) j(a) = а, j(b) = b
2) j(t) и j¢(t) непрерывны на отрезке [a, b]
3) f(j(t)) определена на отрезке [a, b], то
, где f(x) – непрерывная функция на отрезке [a, b].
Введем новую переменную в соответствии с формулой x = j(t).
Тогда если
1) j(a) = а, j(b) = b
2) j(t) и j¢(t) непрерывны на отрезке [a, b]
3) f(j(t)) определена на отрезке [a, b], то
 Тогда
Тогда  Пример.
Пример.
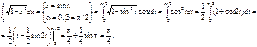 При замене переменной в определенном интеграле следует помнить о том, что вводимая функция (в рассмотренном примере это функция sin) должна быть непрерывна на отрезке интегрирования. В противном случае формальное применение формулы приводит к абсурду.
Пример.
При замене переменной в определенном интеграле следует помнить о том, что вводимая функция (в рассмотренном примере это функция sin) должна быть непрерывна на отрезке интегрирования. В противном случае формальное применение формулы приводит к абсурду.
Пример.
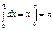 , с другой стороны, если применить тригонометрическую подстановку,
, с другой стороны, если применить тригонометрическую подстановку,
 Т.е. два способа нахождения интеграла дают различные результаты. Это произошло из-за того, что не был учтен тот факт, что введенная переменная tgx имеет на отрезке интегрирования разрыв (в точке х = p/2). Поэтому в данном случае такая подстановка неприменима. При замене переменной в определенном интеграле следует внимательно следить за выполнением перечисленных выше условий.
Интегрирование по частям.
Если функции u = j(x) и v = y(x) непрерывны на отрезке [a, b], а также непрерывны на этом отрезке их производные, то справедлива формула интегрирования по частям:
Т.е. два способа нахождения интеграла дают различные результаты. Это произошло из-за того, что не был учтен тот факт, что введенная переменная tgx имеет на отрезке интегрирования разрыв (в точке х = p/2). Поэтому в данном случае такая подстановка неприменима. При замене переменной в определенном интеграле следует внимательно следить за выполнением перечисленных выше условий.
Интегрирование по частям.
Если функции u = j(x) и v = y(x) непрерывны на отрезке [a, b], а также непрерывны на этом отрезке их производные, то справедлива формула интегрирования по частям:
 Вывод этой формулы абсолютно аналогичен выводу формулы интегрирования по частям для неопределенного интеграла, который был весьма подробно рассмотрен выше, поэтому здесь приводить его нет смысла.
Вывод этой формулы абсолютно аналогичен выводу формулы интегрирования по частям для неопределенного интеграла, который был весьма подробно рассмотрен выше, поэтому здесь приводить его нет смысла.
 |
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 561; Нарушение авторских прав?; Мы поможем в написании вашей работы!