
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
|
Нахождение площади криволинейного сектора
Вычисление площадей плоских фигур.
+ +
0 a - b x
Известно, что определенный интеграл на отрезке представляет собой площадь криволинейной трапеции, ограниченной графиком функции f(x). Если график расположен ниже оси Ох, т.е. f(x) < 0, то площадь имеет знак “-“, если график расположен выше оси Ох, т.е. f(x) > 0, то площадь имеет знак “+”.
Для нахождения суммарной площади используется формула 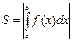 . .
Площадь фигуры, ограниченной некоторыми линиями может быть найдена с помощью определенных интегралов, если известны уравнения этих линий.
Пример. Найти площадь фигуры, ограниченной линиями y = x, y = x2, x = 2.

Искомая площадь (заштрихована на рисунке) может быть найдена по формуле:
 (ед2) (ед2)

r = f(j)
b
a
О r
Для нахождения площади криволинейного сектора введем полярную систему координат. Уравнение кривой, ограничивающей сектор в этой системе координат, имеет вид r = f(j), где r - длина радиус – вектора, соединяющего полюс с произвольной точкой кривой, а j - угол наклона этого радиус – вектора к полярной оси.
Подробнее о полярной системе координат и ее связи с декартовой прямоугольной системой координат см. Полярная система координат. “Курс высшей математики. Часть 1.”
Площадь криволинейного сектора может быть найдена по формуле
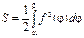
| Билет№45
 Вычисление длины дуги кривой.
y y = f(x)
DSi Dyi
Dxi
a b x
Длина ломаной линии, которая соответствует дуге, может быть найдена как Вычисление длины дуги кривой.
y y = f(x)
DSi Dyi
Dxi
a b x
Длина ломаной линии, которая соответствует дуге, может быть найдена как 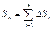 .
Тогда длина дуги равна .
Тогда длина дуги равна 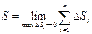 .
Из геометрических соображений: .
Из геометрических соображений:  В то же время
В то же время  Тогда можно показать (см. Интегрируемая функция.), что
Тогда можно показать (см. Интегрируемая функция.), что
 Т.е.
Т.е. 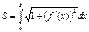 Если уравнение кривой задано параметрически, то с учетом правил вычисления производной параметрически заданной функции (см. Производная фунции, заданной параметрически.), получаем
Если уравнение кривой задано параметрически, то с учетом правил вычисления производной параметрически заданной функции (см. Производная фунции, заданной параметрически.), получаем
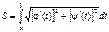 ,
где х = j(t) и у = y(t).
Если задана пространственная кривая, и х = j(t), у = y(t) и z = Z(t), то ,
где х = j(t) и у = y(t).
Если задана пространственная кривая, и х = j(t), у = y(t) и z = Z(t), то
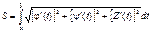 Если кривая задана в полярных координатах, то
Если кривая задана в полярных координатах, то
 , r = f(j).
Пример: Найти длину окружности, заданной уравнением x2 + y2 = r2.
1 способ.Выразим из уравнения переменную у. , r = f(j).
Пример: Найти длину окружности, заданной уравнением x2 + y2 = r2.
1 способ.Выразим из уравнения переменную у. 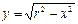 Найдем производную
Найдем производную  Тогда
Тогда 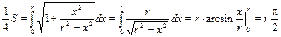 Тогда S = 2pr. Получили общеизвестную формулу длины окружности.
2 способ. Если представить заданное уравнение в полярной системе координат, то получим: r2cos2j + r2sin2j = r2, т.е. функция r = f(j) = r,
Тогда S = 2pr. Получили общеизвестную формулу длины окружности.
2 способ. Если представить заданное уравнение в полярной системе координат, то получим: r2cos2j + r2sin2j = r2, т.е. функция r = f(j) = r,  тогда тогда
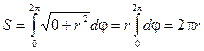
|
Билет№46
Площадь поверхности тела вращения.
 Мi B
А
х
xi
Определение: Площадью поверхности вращения кривой АВ вокруг данной оси называют предел, к которому стремятся площади поверхностей вращения ломаных, вписанных в кривую АВ, при стремлении к нулю наибольших из длин звеньев этих ломаных.
Разобьем дугу АВ на n частей точками M0, M1, M2, …, Mn. Координаты вершин полученной ломаной имеют координаты xi и yi. При вращении ломаной вокруг оси получим поверхность, состоящую из боковых поверхностей усеченных конусов, площадь которых равна DPi. Эта площадь может быть найдена по формуле: Мi B
А
х
xi
Определение: Площадью поверхности вращения кривой АВ вокруг данной оси называют предел, к которому стремятся площади поверхностей вращения ломаных, вписанных в кривую АВ, при стремлении к нулю наибольших из длин звеньев этих ломаных.
Разобьем дугу АВ на n частей точками M0, M1, M2, …, Mn. Координаты вершин полученной ломаной имеют координаты xi и yi. При вращении ломаной вокруг оси получим поверхность, состоящую из боковых поверхностей усеченных конусов, площадь которых равна DPi. Эта площадь может быть найдена по формуле:
 Здесь DSi – длина каждой хорды.
Здесь DSi – длина каждой хорды.
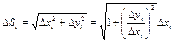 Применяем теорему Лагранжа (см. Теорема Лагранжа.) к отношению
Применяем теорему Лагранжа (см. Теорема Лагранжа.) к отношению 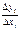 .
Получаем: .
Получаем: 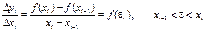 Тогда
Тогда 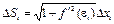
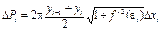 Площадь поверхности, описанной ломаной равна:
Площадь поверхности, описанной ломаной равна:
 Эта сумма не является интегральной, но можно показать, что
Эта сумма не является интегральной, но можно показать, что
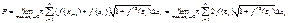 Тогда
Тогда 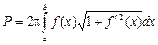 - формула вычисления площади поверхности тела вращения. - формула вычисления площади поверхности тела вращения.
| Билет№47
Несобственные интегралы.
Пусть функция f(x) определена и непрерывна на интервале [a, ¥). Тогда она непрерывна на любом отрезке [a, b].
Определение: Если существует конечный предел  , то этот предел называется несобственным интегралом от функции f(x) на интервале [a, ¥).
Обозначение: , то этот предел называется несобственным интегралом от функции f(x) на интервале [a, ¥).
Обозначение: 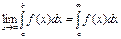 Если этот предел существуетиконечен, то говорят, что несобственный интеграл сходится.
Если предел не существует или бесконечен, то несобственный интеграл расходится.
Аналогичные рассуждения можно привести для несобственных интегралов вида:
Если этот предел существуетиконечен, то говорят, что несобственный интеграл сходится.
Если предел не существует или бесконечен, то несобственный интеграл расходится.
Аналогичные рассуждения можно привести для несобственных интегралов вида:
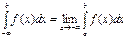
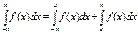 Конечно, эти утверждения справедливы, если входящие в них интегралы существуют.
Пример.
Конечно, эти утверждения справедливы, если входящие в них интегралы существуют.
Пример.
 - не существует.
Несобственный интеграл расходится.
Пример. - не существует.
Несобственный интеграл расходится.
Пример.
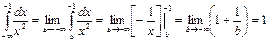 - интеграл сходится
Теорема: Если для всех х (x ³ a) выполняется условие - интеграл сходится
Теорема: Если для всех х (x ³ a) выполняется условие 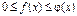 и интеграл и интеграл  сходится, то сходится, то 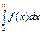 тоже сходится и тоже сходится и 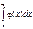 ³ ³  .
Теорема: Если для всех х (x ³ a) выполняется условие .
Теорема: Если для всех х (x ³ a) выполняется условие 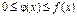 и интеграл и интеграл  расходится, то расходится, то 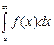 тоже расходится.
Теорема: Если тоже расходится.
Теорема: Если  сходится, то сходится и интеграл сходится, то сходится и интеграл 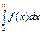 .
В этом случае интеграл .
В этом случае интеграл  называется абсолютно сходящимся. называется абсолютно сходящимся.
|
| ВОПРОСЫ К ЭКЗАМЕНУ
1. Определители. Их свойства. Вычисления. Доказательство свойств.
2. Исследование и решение систем линейных уравнений по формулам Крамера. Вывод формулы Крамера в случае единственного решения.
3. Однородные системы линейных уравнений, их исследование.
4. Матрицы, их виды. Линейные операции, их свойства.
5. Умножение матриц. Следствия.
6. Обратные матрицы. Решение систем линейных уравнений с помощью обратной матрицы Исследование решений. Теорема Кронекера-Капелли. Ранг матрицы, свойства ранга.
7. Векторы, их виды. Линейные операции. Свойства.
8Понятие линейной зависимости векторов. Базис. Разложение по базису.
9. Ортонормированный (декартов) базис в пространствах R2, R3. Координаты вектора и его проекции в этом базисе, модуль вектора, его направление.
10. Скалярное произведение векторов в пространствах R.2 и R3, Механический и геометрический смысл, свойства. Условие ортогональности векторов, угол между векторами.
11. Векторное произведение векторов в пространстве R3, свойства, геометрический смысл. Выражение в декартовых координатах. Механические (момент сппц относительно точки) и геометрические приложения. Условия коллинеарности векторов.
12. Смешанное произведение векторов в пространстве R", свойства, геометрический смысл. Выражение в декартовых координатах. Условие компланарности векторов. Геометрические приложения.
13. Вывод уравнений прямой на плоскости (векторного, нормального, общего). Вывод других уравнений (в отрезках, с угловым коэффициентом, через две точки, через точку с заданным нормальным вектором и другие). Взаимное расположение прямых, угол между ними.
14. Геометрический смысл уравнений первой степени с тремя переменными. Вывод уравнений плоскости в пространстве R3 (векторного, нормального, общего). Вывод других уравнений (в отрезках, через три точки, через точку с заданным нормальным вектором и других). Взаимное расположение плоскостей (геометрический смысл) Исследование общего уравнения. Расстояние от точки до плоскости.
15. Прямая в пространстве, вывод общих уравнений, канонических, через две точки и других Связь общих уравнений с каноническими. Взаимное расположение прямых, угол между ними, кратчайшее расстояние от точки до прямой.
16. Расстояние между двумя точками в пространствах R и R. Деление отрезка в данном отношении.
17. Приведение уравнений кривых к каноническому виду.
18. Числовые последовательности. Способы задания. Виды числовых последовательностей.
19. Понятие о функции. Способы задания. Обратная функция. Предел функции. Односторонние пределы.
20. Свойства ограниченных функций. Бесконечно малая и бесконечно большая функции. Связь между ними.
21. Теорема о пределах. Раскрытие неопределенностей
22. Первый замечательный предел. Следствия.
23. Второй замечательный предел. Следствия.
24 Сравнение бесконечно-малых. Эквивалентные бесконечно-малые.
2. Непрерывность функций. Необходимые и достаточные условия. Определения. Разрывы. Виды точек разрыва. Свойства непрерывных функций. Непрерывность сложной функции. Раскрытие
неопределенностей вида 1 ".
26 Производная функции. Определения. Геометрический и физический смысл. Примеры. Условия существования производной функции в точке. Связь дифференцируемости и непрерывности. Правила дифференцирования. Следствия.
27. Производная сложной и обратной функций (две теоремы с доказательствами). Производная показательной, логарифмической, степенной функций.
28. Производные тригонометрических и обратных тригонометрических функций.
29. Логарифмическое дифференцирование. Производная степенно-показательной функции.
30. Дифференциал функции. Определение. Геометрический смысл. Формула приближенных вычислений. Вычисления. Инвариантность формы.
31. Основные теоремы дифференциального исчисления (Вейрштрасса, Ролля, Лагранжа).
32. Теорема Коши. Правило Лопиталя.
Раскрытие неопределенностей 0 • соз со — соз 1СО,0,оо
33. Монотонность функции. Признаки существования экстремума.
34. Выпуклость, вогнутость графика функции. Точки перегиба. Асимптоты графика. Общая схема исследования функции.
35. Первообразная функция. Неопределенный интеграл. Свойства. Геометрический смысл. Основная таблица неопределенных интегралов.
36. Методы интегрирования (непосредственного интегрирования, подстановки, по частям). Примеры.
37. Интегрирование рациональных выражений. Простейшие рациональные дроби Метод неопределенных коэффициентов разложения правильной рациональной дроби на простейшие.
38. Интегрирование простейших рациональных дробей. Рекуррентная формула.
39. Интегрирование тригонометрических выражений.
40. Интегрирование иррациональных выражений. Подстановки Эйлера. Интегрирование биномиального дифференциала.
41. Определенный интеграл, свойства. Теорема о среднем. Интеграл от четных и нечетных функций.
42. Определенный интеграл с переменным верхним пределом. Формула Ньютона-Лейбница вычисления определенных интегралов.
43. Методы вычисления определенного интеграла (замена переменной, по частям). Привести примеры.
44. Геометрические приложения определенного интеграла (площади при различном задании кривой - декартовым уравнением, параметрическими уравнениями, полярным уравнением).
45. Вычисление длины плоской и пространственной линии (при различном задании: декартовым уравнением, полярным уравнением). Дифференциал дуги.
46. Вычисление поверхности вращения с помощью определенного интеграла.
47.Несобственные интегралы 1го и 2-го рода.
| |

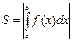 .
.

 (ед2)
(ед2)
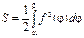
 Вычисление длины дуги кривой.
y y = f(x)
DSi Dyi
Dxi
a b x
Длина ломаной линии, которая соответствует дуге, может быть найдена как
Вычисление длины дуги кривой.
y y = f(x)
DSi Dyi
Dxi
a b x
Длина ломаной линии, которая соответствует дуге, может быть найдена как 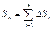 .
Тогда длина дуги равна
.
Тогда длина дуги равна 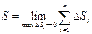 .
Из геометрических соображений:
.
Из геометрических соображений:  В то же время
В то же время  Тогда можно показать (см. Интегрируемая функция.), что
Тогда можно показать (см. Интегрируемая функция.), что
 Т.е.
Т.е. 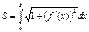 Если уравнение кривой задано параметрически, то с учетом правил вычисления производной параметрически заданной функции (см. Производная фунции, заданной параметрически.), получаем
Если уравнение кривой задано параметрически, то с учетом правил вычисления производной параметрически заданной функции (см. Производная фунции, заданной параметрически.), получаем
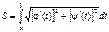 ,
где х = j(t) и у = y(t).
Если задана пространственная кривая, и х = j(t), у = y(t) и z = Z(t), то
,
где х = j(t) и у = y(t).
Если задана пространственная кривая, и х = j(t), у = y(t) и z = Z(t), то
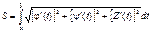 Если кривая задана в полярных координатах, то
Если кривая задана в полярных координатах, то
 , r = f(j).
Пример: Найти длину окружности, заданной уравнением x2 + y2 = r2.
1 способ.Выразим из уравнения переменную у.
, r = f(j).
Пример: Найти длину окружности, заданной уравнением x2 + y2 = r2.
1 способ.Выразим из уравнения переменную у. 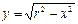 Найдем производную
Найдем производную  Тогда
Тогда 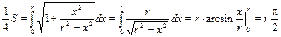 Тогда S = 2pr. Получили общеизвестную формулу длины окружности.
2 способ. Если представить заданное уравнение в полярной системе координат, то получим: r2cos2j + r2sin2j = r2, т.е. функция r = f(j) = r,
Тогда S = 2pr. Получили общеизвестную формулу длины окружности.
2 способ. Если представить заданное уравнение в полярной системе координат, то получим: r2cos2j + r2sin2j = r2, т.е. функция r = f(j) = r,  тогда
тогда
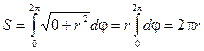
 Мi B
А
х
xi
Определение: Площадью поверхности вращения кривой АВ вокруг данной оси называют предел, к которому стремятся площади поверхностей вращения ломаных, вписанных в кривую АВ, при стремлении к нулю наибольших из длин звеньев этих ломаных.
Разобьем дугу АВ на n частей точками M0, M1, M2, …, Mn. Координаты вершин полученной ломаной имеют координаты xi и yi. При вращении ломаной вокруг оси получим поверхность, состоящую из боковых поверхностей усеченных конусов, площадь которых равна DPi. Эта площадь может быть найдена по формуле:
Мi B
А
х
xi
Определение: Площадью поверхности вращения кривой АВ вокруг данной оси называют предел, к которому стремятся площади поверхностей вращения ломаных, вписанных в кривую АВ, при стремлении к нулю наибольших из длин звеньев этих ломаных.
Разобьем дугу АВ на n частей точками M0, M1, M2, …, Mn. Координаты вершин полученной ломаной имеют координаты xi и yi. При вращении ломаной вокруг оси получим поверхность, состоящую из боковых поверхностей усеченных конусов, площадь которых равна DPi. Эта площадь может быть найдена по формуле:
 Здесь DSi – длина каждой хорды.
Здесь DSi – длина каждой хорды.
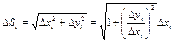 Применяем теорему Лагранжа (см. Теорема Лагранжа.) к отношению
Применяем теорему Лагранжа (см. Теорема Лагранжа.) к отношению 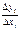 .
Получаем:
.
Получаем: 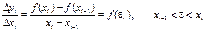 Тогда
Тогда 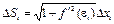
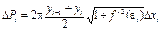 Площадь поверхности, описанной ломаной равна:
Площадь поверхности, описанной ломаной равна:
 Эта сумма не является интегральной, но можно показать, что
Эта сумма не является интегральной, но можно показать, что
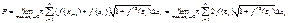 Тогда
Тогда 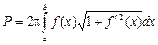 - формула вычисления площади поверхности тела вращения.
- формула вычисления площади поверхности тела вращения.
 , то этот предел называется несобственным интегралом от функции f(x) на интервале [a, ¥).
Обозначение:
, то этот предел называется несобственным интегралом от функции f(x) на интервале [a, ¥).
Обозначение: 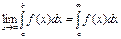 Если этот предел существуетиконечен, то говорят, что несобственный интеграл сходится.
Если предел не существует или бесконечен, то несобственный интеграл расходится.
Аналогичные рассуждения можно привести для несобственных интегралов вида:
Если этот предел существуетиконечен, то говорят, что несобственный интеграл сходится.
Если предел не существует или бесконечен, то несобственный интеграл расходится.
Аналогичные рассуждения можно привести для несобственных интегралов вида:
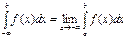
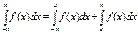 Конечно, эти утверждения справедливы, если входящие в них интегралы существуют.
Пример.
Конечно, эти утверждения справедливы, если входящие в них интегралы существуют.
Пример.
 - не существует.
Несобственный интеграл расходится.
Пример.
- не существует.
Несобственный интеграл расходится.
Пример.
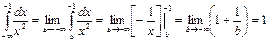 - интеграл сходится
Теорема: Если для всех х (x ³ a) выполняется условие
- интеграл сходится
Теорема: Если для всех х (x ³ a) выполняется условие 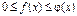 и интеграл
и интеграл  сходится, то
сходится, то 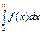 тоже сходится и
тоже сходится и 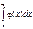 ³
³  .
Теорема: Если для всех х (x ³ a) выполняется условие
.
Теорема: Если для всех х (x ³ a) выполняется условие 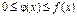 и интеграл
и интеграл  расходится, то
расходится, то 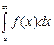 тоже расходится.
Теорема: Если
тоже расходится.
Теорема: Если  сходится, то сходится и интеграл
сходится, то сходится и интеграл 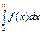 .
В этом случае интеграл
.
В этом случае интеграл  называется абсолютно сходящимся.
называется абсолютно сходящимся.