Бинарное дерево. Основные определения и понятия. Бинарный поиск по дереву. Формирование бинарного дерева этим методом

END

END

BEGIN

ELSE

END

BEGIN

BEGIN

BEGIN

VAR

BEGIN

ELSE

END

BEGIN

BEGIN

BEGIN

ELSE

BEGIN

VAR

BEGIN

BEGIN

TYPE

POINT=^ZAP;

ZAP=RECORD

INF1: INTEGER; { первое информационное поле }

INF2: STRING; { второе информационное поле }

NEXT:POINT; {ссылочное поле на следующий элемент}

PREV:POINT; {ссылочное поле на предыдущий элемент}

END;

Все действия над элементами списка, приводящие к изменению порядка обработки элементов списка - вставка, удаление, перестановка - сводятся к действиям со ссылками. Сами же элементы не меняют своего физического положения в памяти.

Формирование пустого списка.

PROCEDURE CREATE_EMPTY_LIST (VAR FIRST: EL);

FIRST = NIL;

END;

Формирование очередного элемента списка.

PROCEDURE CREATE_NEW_ELEM(VAR P: EL);

NEW (P);

WRITELN ('ВВЕДИТЕ ЗНАЧЕНИЕ ПЕРВОГО ИНФОРМАЦИОННОГО ПОЛЯ: ');

READLN (P^.INF1);

WRITELN ('ВВЕДИТЕ ЗНАЧЕНИЕ ВТОРОГО ИНФОРМАЦИОННОГО ПОЛЯ: ');

READLN (P^.INF2);

P^.NEXT:= NIL;

{ ВСЕ ПОЛЯ ЭЛЕМЕНТА ДОЛЖНЫ БЫТЬ ИНИЦИАЛИЗИРОВАНЫ }

END;

Подсчет числа элементов списка

FUNCTION COUNT_EL(FIRST:EL):INTEGER;

K: INTEGER;

Q: EL;

IF FIRST = NIL THEN

K:=0 { СПИСОК ПУСТ }

BEGIN {СПИСОК СУЩЕСТВУЕТ}

K:=1; {В СПИСКЕ ЕСТЬ ХОТЯ БЫ ОДИН ЭЛЕМЕНТ}

Q:=FIRST;

{ПЕРЕБОР ЭЛЕМЕНТОВ СПИСКА НАЧИНАЕТСЯ С ПЕРВОГО}

WHILE Q^.NEXT <> NIL DO

K:=K+1;

Q:=Q^.NEXT;

{ПЕРЕХОД К СЛЕДУЮЩЕМУ ЭЛЕМЕНТУ СПИСКА}

END;

END;

COUNT_EL:=K;

END;

Вставка элемента в начало списка.

PROCEDURE INS_BEG_LIST(P: EL; {АДРЕС ВКЛЮЧАЕМОГО ЭЛЕМЕНТА}

VAR FIRST: EL);

IF FIRST = NIL THEN

FIRST:= P;

P^.NEXT:= NIL

P^.NEXT:=FIRST;{ССЫЛКА НА БЫВШИЙ ПЕРВЫМ ЭЛЕМЕНТ}

FIRST:=P;{ ВКЛЮЧАЕМЫЙ ЭЛЕМЕНТ СТАНОВИТСЯ ПЕРВЫМ }

END;

END;

Удаление элемента из начала списка

PROCEDURE DEL_BEG_LIST (VAR FIRST: EL);

P: EL;

ANSWER: STRING;

IF FIRST <> NIL THEN

BEGIN { СПИСОК НЕ ПУСТ }

WRITELN ('ВЫ ХОТИТЕ УДАЛИТЬ ПЕРВЫЙ ЭЛЕМЕНТ?(ДА/НЕТ) ');

READLN (ANSWER);

IF ANSWER = 'ДА' THEN

P:=FIRST;

IF P^.NEXT = NIL THEN {В СПИСКЕ ОДИН ЭЛЕМЕНТ }

DISPOSE (P); {УНИЧТОЖЕНИЕ ЭЛЕМЕНТА}

FIRST:=NIL; {СПИСОК СТАЛ ПУСТЫМ }

P:= FIRST;{АДРЕС УДАЛЯЕМОГО ЭЛЕМЕНТА }

FIRST:=FIRST^.NEXT;

{АДРЕС НОВОГО ПЕРВОГО ЭЛЕМЕНТА}

DISPOSE(P);

{УДАЛЕНИЕ БЫВШЕГО ПЕРВОГО ЭЛЕМЕНТА }

END;

Бинарное (двоичное) дерево (binary tree) – древовидная структура данных, в которой каждый узел имеет не более двух потомков (детей).

Бинарное дерево [др. источник] – это упорядоченное дерево, каждая вершина которого имеет не более двух поддеревьев, причем для каждого узла выполняется правило: в левом поддереве содержатся только ключи, имеющие значения, меньшие, чем значение данного узла, а в правом поддереве содержатся только ключи, имеющие значения, большие, чем значение данного узла.

Бинарное дерево является рекурсивной структурой, поскольку каждое его поддерево само является бинарным деревом и, следовательно, каждый его узел в свою очередь является корнем дерева. Узел дерева, не имеющий потомков, называется листом.

То есть двоичное дерево либо является пустым, либо состоит из данных и двух поддеревьев (каждое из которых может быть пустым). Очевидным, но важным для понимания фактом является то, что каждое поддерево в свою очередь тоже является деревом.

Каждый узел в дереве задаёт поддерево, корнем которого он является.

У вершины n=(data, left, right) есть два ребёнка (левый и правый) left и right и, соответственно, два поддерева (левое и правое) с корнями left и right.

Свойство. Строго бинарное дерево с n листами всегда содержит 2n-1 узлов.

Уровень узла в бинарном дереве: уровень корня всегда равен нулю, а далее номера уровней при движении по дереву от корня увеличиваются на 1 по отношению к своему непосредственному предку.

Глубина бинарного дерева - это максимальный уровень листа дерева, что равно длине самого длинного пути от корня к листу дерева.

Полное бинарное дерево уровня n - это дерево, в котором каждый узел уровня n является листом, и каждый узел уровня меньше n имеет непустые левое и правое поддеревья

Почти полное бинарное дерево - это бинарное дерево, для которого существует неотрицательное целое k такое, что: 1) Каждый лист в дереве имеет уровень k или k+1. 2) Если узел дерева имеет правого потомка уровня k+1, тогда все его левые потомки, являющиеся листами, также имеют уровень k+1.

Упорядоченные бинарные деревья - это деревья, в которых для каждого узла Х выполняется правило: в левом поддереве - ключи, меньшие Х, в правом поддереве - большие или равные Х.

Построение бинарного дерева. Двоичное дерево поиска.

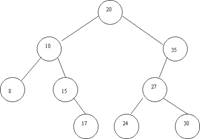Правило построения двоичного дерева поиска: элементы, у которых значение некоторого признака меньше, чем у корня, всегда включаются слева от некоторого поддерева, а элементы со значениями, большими, чем у корня - справа.

Этот принцип используется и при формировании двоичного дерева, и при поиске в нем элементов. Обратить внимание: поиск места подключения очередного элемента всегда начинается с корня.

Пример: 20, 10, 35, 15, 17, 27, 24, 8, 30.

Поиск элемента в бинарном дереве.

При поиске элемента с некоторым значением признака происходит спуск по дереву, начиная от корня, причем выбор ветви следующего шага - направо или налево согласно значению искомого признака - происходит в каждом очередном узле на этом пути.

При поиске элемента результатом будет либо найденный узел с заданным значением признака, либо поиск закончится листом с «нулевой» ссылкой, а требуемый элемент отсутствует на проделанном по дереву пути.

Если поиск был проделан для включения очередного узла в дерево, то в результате будет найден узел с пустой ссылкой (пустыми ссылками), к которому справа или слева в соответствии со значением признака и будет присоединен новый узел.

Двоичное дерево поиска можно определить так:

− Двоичное дерево состоит из узлов (вершин) — записей вида (data, left, right), где data — некоторые данные привязанные к узлу, left и right — ссылки на потомков.

− Данные (data) обладают ключом (key) на котором определена операция сравнения " меньше ". В конкретных реализациях это может быть пара (key, value).

− Для любого узла X выполняются свойства дерева поиска:

key[left[X]] < key[X] ≤ key[right[X]], т. е. ключи данных родительского узла больше ключей данных левого сына и нестрого меньше ключей данных правого.

Основные операции в двоичном дереве поиска:

FIND (K) — поиск узла, в котором хранится пара (key, value) с key = K.

INSERT (K,V) — добавление в дерево пары (key, value) = (K, V).

REMOVE (K) — удаление узла, в котором хранится пара (key, value) с key = K.

Дата добавления: 2015-04-24