Рекурсия при работе со списками и деревьями. Очередь, стек, дек как формы работы со списком, действия над ними

Бинарное дерево. Основные операции с бинарными деревьями. Способы обхода бинарного дерева. Варианты поиска по бинарному дереву

Бинарное (двоичное) дерево (binary tree) – древовидная структура данных, в которой каждый узел имеет не более двух потомков (детей).

Бинарное дерево [др. источник] – это упорядоченное дерево, каждая вершина которого имеет не более двух поддеревьев, причем для каждого узла выполняется правило: в левом поддереве содержатся только ключи, имеющие значения, меньшие, чем значение данного узла, а в правом поддереве содержатся только ключи, имеющие значения, большие, чем значение данного узла.

Бинарное дерево является рекурсивной структурой, поскольку каждое его поддерево само является бинарным деревом и, следовательно, каждый его узел в свою очередь является корнем дерева. Узел дерева, не имеющий потомков, называется листом.

То есть двоичное дерево либо является пустым, либо состоит из данных и двух поддеревьев (каждое из которых может быть пустым). Очевидным, но важным для понимания фактом является то, что каждое поддерево в свою очередь тоже является деревом.

Каждый узел в дереве задаёт поддерево, корнем которого он является.

У вершины n=(data, left, right) есть два ребёнка (левый и правый) left и right и, соответственно, два поддерева (левое и правое) с корнями left и right.

Свойство. Строго бинарное дерево с n листами всегда содержит 2n-1 узлов.

Уровень узла в бинарном дереве: уровень корня всегда равен нулю, а далее номера уровней при движении по дереву от корня увеличиваются на 1 по отношению к своему непосредственному предку.

Глубина бинарного дерева - это максимальный уровень листа дерева, что равно длине самого длинного пути от корня к листу дерева.

Полное бинарное дерево уровня n - это дерево, в котором каждый узел уровня n является листом, и каждый узел уровня меньше n имеет непустые левое и правое поддеревья

Почти полное бинарное дерево - это бинарное дерево, для которого существует неотрицательное целое k такое, что: 1) Каждый лист в дереве имеет уровень k или k+1. 2) Если узел дерева имеет правого потомка уровня k+1, тогда все его левые потомки, являющиеся листами, также имеют уровень k+1.

Упорядоченные бинарные деревья - это деревья, в которых для каждого узла Х выполняется правило: в левом поддереве - ключи, меньшие Х, в правом поддереве - большие или равные Х.

Построение бинарного дерева. Двоичное дерево поиска.

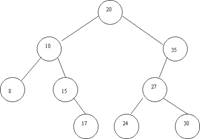Правило построения двоичного дерева поиска: элементы, у которых значение некоторого признака меньше, чем у корня, всегда включаются слева от некоторого поддерева, а элементы со значениями, большими, чем у корня - справа.

Этот принцип используется и при формировании двоичного дерева, и при поиске в нем элементов. Обратить внимание: поиск места подключения очередного элемента всегда начинается с корня.

Пример: 20, 10, 35, 15, 17, 27, 24, 8, 30.

Основные операции в двоичном дереве поиска:

FIND (K) — поиск узла, в котором хранится пара (key, value) с key = K.

INSERT (K,V) — добавление в дерево пары (key, value) = (K, V).

REMOVE (K) — удаление узла, в котором хранится пара (key, value) с key = K.

Способы обхода бинарного дерева (TRAVERSE).

− в симметричном порядке

INFIX _TRAVERSE (f) — обойти всё дерево, следуя порядку (левое поддерево, вершина, правое поддерево).

− в прямом порядке

PREFIX _TRAVERSE (f) — обойти всё дерево, следуя порядку (вершина, левое поддерево, правое поддерево).

− в обратном порядке

POSTFIX _TRAVERSE (f) — обойти всё дерево, следуя порядку (левое поддерево, правое поддерево, вершина)

Поиск элемента в бинарном дереве.

При поиске элемента с некоторым значением признака происходит спуск по дереву, начиная от корня, причем выбор ветви следующего шага - направо или налево согласно значению искомого признака - происходит в каждом очередном узле на этом пути.

При поиске элемента результатом будет либо найденный узел с заданным значением признака, либо поиск закончится листом с «нулевой» ссылкой, а требуемый элемент отсутствует на проделанном по дереву пути.

Если поиск был проделан для включения очередного узла в дерево, то в результате будет найден узел с пустой ссылкой (пустыми ссылками), к которому справа или слева в соответствии со значением признака и будет присоединен новый узел.

Рекурсия.

Метод P (процедура или функция) называется рекурсивным, если при выполнении тела метода происходит вызов метода P.

Дерево. Рекурсивное определение.

Дерево представляет собой вершину, имеющую ограниченное число связей (ветвей) к другим деревьям. Нижележащие деревья для текущей вершины называются поддеревьями, а их головные вершины - потомками. По отношению к потомкам текущая вершина называется предком. Вершины, не имеющие потомков, называются оконечными или терминальными, головная вершина всего дерева называется корневой. Рекурсивное определение дерева ведет к тому, что алгоритмы работы с ним тоже являются рекурсивными.

Полный рекурсивный обход дерева (не зависит от формы представления дерева). Любое действие, выполняемое над вершиной, должно быть выполнено также и по отношению ко всем его поддеревьям, а значит, алгоритм должен быть рекурсивно выполнен по отношению ко всем потомкам этой вершины. В качестве параметра обязателен идентификатор текущей вершины (индекс, указатель, ссылка).

Дерево называется сбалансированным, если длина максимальной и минимальной ветвей отличается не более чем на 1. Дерево представляет собой компромисс между массивом и списком.

Списки. Общее определение.

Список - это конечное множество динамических элементов, размещающихся в разных областях памяти и объединенных в логически упорядоченную последовательность с помощью специальных указателей (адресов связи).

Список - структура данных, в которой каждый элемент имеет информационное поле (поля) и ссылку (ссылки), то есть адрес (адреса), на другой элемент (элементы) списка.

Списки. Рекурсивное определение.

Список - структура данных: 1) пустой список ([ ]) является списком; 2) структура вида [H|T] является списком, если H — первый элемент списка (или несколько первых элементов списка, перечисленных через запятую), а T — список, состоящий из оставшихся элементов исходного списка.

Рекурсивная обработка списков

Данное определение позволяет организовывать рекурсивную обработку списков, разделяя непустой список на голову и хвост. Хвост, в свою очередь, также является списком, содержащим меньшее количество элементов, чем исходный список. Если хвост не пуст, его также можно разбить на голову и хвост. И так до тех пор, пока мы не доберемся до пустого списка, у которого нет головы.

Рекурсия является одним из удобнейших средств при работе с линейными списками. Она позволяет сократить код программы и сделать алгоритмы обхода узлов деревьев и списков более понятными.

Стеки, деки, очереди.

Стек (англ. stack — стопка) — структура данных (упорядоченный набор элементов), в которой доступ к элементам организован по принципу LIFO (англ. last in — first out, «последним пришёл — первым вышел»).

Операции над стеком:

1) добавление в стек нового элемента;

2) определение пуст ли стек;

3) доступ к последнему включенному элементу, вершине стека;

4) исключение из стека последнего включенного элемента.

Добавление элемента (проталкиванием - push), возможно только в вершину стека (добавленный элемент становится первым сверху). Удаление элемента (выталкивание - pop), тоже возможно только из вершины стека, при этом второй сверху элемент становится верхним.

Такая структура данных очень хорошо реализуется с помощью списка. Для стека может подойти линейный однонаправленный список без головного элемента со вставкой и исключением элементов в начале списка (это и будет вершиной стека).

Очередь — структура данных с дисциплиной доступа к элементам «первый пришёл — первый вышел» (FIFO, First In — First Out).

Операции над очередью:

1) добавление в конец очереди нового элемента;

2) определение пуста ли очередь;

3) доступ к первому элементу очереди;

4) исключение из очереди первого элемента.

Добавление элемента (принято обозначать словом enqueue — поставить в очередь) возможно лишь в конец очереди, выборка — только из начала очереди (что принято называть словом dequeue — убрать из очереди), при этом выбранный элемент из очереди удаляется.

Для реализации очереди необходим список, для которого известны адрес первого и адрес последнего элементов.

Очередь может представляться в качестве линейного списка, для которого известны адрес первого и адрес последнего элементов и в котором добавление/удаление элементов идет строго с соответствующих его концов.

Дек (от англ. deq - double ended queue, т.е. очередь с двумя концами) – очередь с двойным доступом – двухконечный стек - это такой последовательный список, в котором как включение, так и исключение элементов может осуществляться с обоих концов списка.

Операции над деком:

1) включение элемента справа;

2) включение элемента слева;

3) исключение элемента справа;

4) исключение элемента слева;

5) определение размера (проверка наличия элементов);

6) очистка.

21. Тестирование. Понятие и цель тестирования. Правильное и неправильное определение тестирования. Основные определения. Тестирование методом «чёрного ящика». Тестирование методом «белого ящика»

Тестирование применяется для определения соответствия предмета испытания заданным спецификациям. В задачи тестирования не входит определение причин несоответствия заданным требованиям (спецификациям).

Тестирование программного обеспечения — процесс исследования программного обеспечения (ПО) с целью получения информации о качестве продукта.

Тестирование – неправильное определение – процесс подтверждения корректности работы программы и демонстрация отсутствия ошибок в программе. Тестирование – процесс разрушительный. Отсюда следует, что тест считается удачным, когда с его помощью обнаружена ошибка.

Отладка (debug, debugging)– процесс поиска, локализации и исправления ошибок в программе. Тестирование – процесс многократного повторения программы с целью обнаружения ошибок. Тестирование – составная часть отладки.

Критерии тестирования.

Поскольку исчерпывающее структурное тестирование невозможно, необходимо выбрать такие критерии его полноты, которые допускали бы их простую проверку и облегчали бы целенаправленный подбор тестов. Наиболее слабым из критериев полноты структурного тестирования является требование хотя бы однократного выполнения каждого оператора программы. Более сильным критерием является критерий: каждая ветвь алгоритма (каждый переход) должна быть пройдена (выполнена) хотя бы один раз.

Уровни тестирования.

1. Модульное тестирование (юнит-тестирование) — тестируется минимально возможный для тестирования компонент, например, отдельный класс или функция.

2. Интеграционное тестирование — тестируются интерфейсы между компонентами, подсистемами.

3. Системное тестирование — тестируется интегрированная система на её соответствие требованиям.

4. Альфа-тестирование — имитация реальной работы с системой штатными разработчиками, либо реальная работа с системой потенциальными пользователями/заказчиком..

5. Бета-тестирование — в некоторых случаях выполняется распространение версии с ограничениями (по функциональности или времени работы) для некоторой группы лиц, с тем чтобы убедиться, что продукт содержит достаточно мало ошибок.

Часто для свободного/открытого ПО стадия альфа-тестирования характеризует функциональное наполнение кода, а бета-тестирования — стадию исправления ошибок. При этом, как правило, на каждом этапе разработки промежуточные результаты работы доступны конечным пользователям.

Методы тестирования ПО:

1) Статическое тестирование – ручная проверка программы за сто-лом.

2) Детерминированное тестирование – при различных комбинациях исходных данных.

3) Стохастическое – исходные данные выбираются произвольно, на выходе определяется качественное совпадение результатов или примерная оценка.

Тестирование по стратегии чёрного ящика.

" Чёрный ящик " - тестирование функционального поведения программы с точки зрения внешнего мира (текст программы не используется). Под «чёрным ящиком» понимается объект исследования, внутреннее устройство которого неизвестно.

В этой стратегии программа рассматривается как чёрный ящик. Целью тестирования ставится выяснение обстоятельств, в которых поведение программы не соответствует спецификации. Для обнаружения всех ошибок в программе необходимо выполнить исчерпывающее тестирование, то есть тестирование на всевозможных наборах данных.

Таким способом невозможно найти взаимоуничтожающихся ошибок. Некоторые ошибки возникают достаточно редко (ошибки работы с памятью) и потому их трудно найти и воспроизвести.

Методы стратегии чёрного ящика:

1. Эквивалентное разбиение. Разработка тестов этим методом осуществляется в два этапа: выделение классов эквивалентности и построение теста.

2. Анализ граничных значений. Граничные условия — это ситуации, возникающие на высших и нижних границах входных классов эквивалентности.

3. Анализ причинно-следственных связей.

4. Предположение об ошибке.

Тестирование по стратегии белого ящика.

"Белый ящик" - тестирование кода на предмет логики работы программы и корректности её работы с точки зрения компилятора того языка, на котором она писалась.

Стратегия тестирования по принципу белого ящика (стратегия тестирования, управляемая логикой программы) позволяет проверить внутреннюю структуру программы. Исходя из этой стратегии, тестировщик получает тестовые данные путем анализа логики работы программы. Трудностью метода белого ящика является сложность отслеживания вычислений времени выполнения.

Методы стратегии белого ящика:

1. Покрытие операторов. Критерии покрытия операторов подразумевает выполнение каждого оператора программы, по крайней мере, один раз.

2. Покрытие решений. В соответствии с этим критерием необходимо составить такое число тестов, при которых каждое условие в программе примет как истинное значение, так и ложное значение.

3. Покрытие условий. Записывается число тестов достаточное для того, чтобы все возможные результаты каждого условия в решении были выполнены, по крайней мере, один раз.

4. Покрытие решений и условий. В соответствии с этим критерием необходимо составить тесты так, чтобы результаты каждого условия выполнялись хотя бы один раз, результаты каждого решения так же выполнялись хотя бы один раз, и каждый оператор должен быть выполнен хотя бы один раз.

5. Комбинаторное покрытие условий. Это критерий требует, чтобы все возможные комбинации результатов условий в каждом решении, а также каждый оператор выполнились, по крайней мере, один раз.

Дата добавления: 2015-04-24