Метод исключения Гаусса без перестановки строк

На 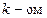этапе нужно выполнить следующие шаги:

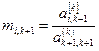
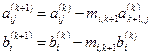
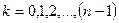
В результате мы получим верхнюю треугольную матрицу .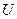

При этом левая треугольная матрица в разложении может быть записана:

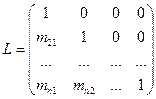
Нижняя треугольная матрица с единицами на главной диагонали, называется нижней унитреугольной матрицей.

Аналогично, верхняя треугольная матрица с единицами на главной диагонали, называется верхней унитреугольной матрицей.

С помощью первой элементарной операции, заключающейся в вычитании строк мы привели расширенную матрицу к виду, состоящему из верхней треугольной матрицы и вектора, представляющего правую часть преобразованного уравнения.

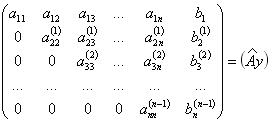
Верхний индекс обозначает номер преобразования.

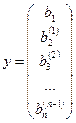
Матрица является нижней треугольной матрицей и решение преобразованной системы может быть получено методом обратной подстановки.

Верхняя треугольная матрица .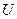

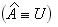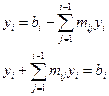
При верхний предел суммирования равен нулю.

Матрица с коэффициентами является нижней унитреугольной.

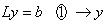
Решение этой системы осуществляется методом прямой подстановки.

После нахождения вектора y находится решение

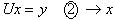
Эти системы являются эквивалентными, а, значит, их решения совпадают.

Эквивалентность систем следует из того, что преобразование матриц осуществляется с помощью первой элементарной операции: вычитание строк, умноженных на некоторые коэффициенты.

Коэффициенты матрицы L вычисляются по формуле:

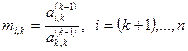
Для того, чтобы операция исключения Гаусса без перестановки строк могла быть осуществлена, необходимо, чтобы все коэффициенты 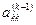отличались от нуля, это необходимо, чтобы могло быть осуществлено деление.

Необходимое условие того, что это не произойдет, заключается в теореме о LU­ -разложении.

Если матрица A имеет невырожденными все ведущие главные подматрицы , то матрица A единственным образом разлагается в произведение матриц L и U.

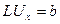
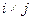Ведущая главная подматрица матрицы – матрица порядка , образованная из элементов матрицы А, стоящих на пересечении первых j и первых i строк.

Этот метод является частным случаем метода подстановок Гаусса.

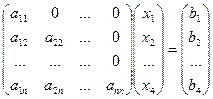
Определители верхней и нижней треугольной матрицы равен произведению диагональных элементов матрицы:

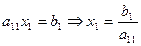
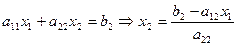
Пример в MathLab:

for i = 1:n;

for j = 1:n-1;

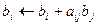
остановка (система вырождена)

Количество операций:

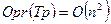
Рассмотренный метод – метод подстановки по строкам.

Если первые k компонентов вектора b будут равны нулю, то число операций уменьшится до .

Модификацией этого метода является метод прямой подстановки по столбцам.

В методе прямой подстановки по столбцам осуществляется последовательное понижение порядка системы уравнений с помощью разбиения матрицы на блоки.

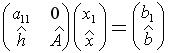
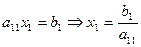
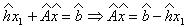
– сложность алгоритма.

for i = 1:n;

система несовместная

for j = i+1:n

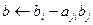
Решение системы с верхней треугольной матрицей производится аналогичными способами вверх.

Дата добавления: 2015-04-24