Графическое решение

Пример 3.1

Графический метод решения задачи линейного программирования

Если число переменных в задаче линейного программирования (ЗЛП) равно двум, а ограничениями является система неравенств, то задачу можно решать графическим методом.

При продаже двух видов товара используется 4 типа ресурсов. Норма затрат ресурсов на реализацию единицы товара, общий объем каждого ресурса заданы в табл. 3.2.

Прибыль от реализации одной единицы товара первого вида составляет 2 усл. ед., второго вида – 3 усл. ед.

Требуется найти оптимальный план реализации товаров, обеспечивающий торговому предприятию максимальную прибыль.

Таблица 3.2

Ресурсы	Норма затрат ресурсов на товары	Общее количество ресурсов
	1 -го вида	2-го вида

Решение

Это задача составления плана реализации товара при n= 2, m =4.

Математическая модель имеет вид

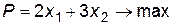(3.16)

В модели управляющие переменные х₁,х₂ – количество реализуемых изделий первого и второго вида, соответственно, Р – прибыль. Система неравенств включает ограничения по ресурсам. Количество ресурсов на реализацию товаров первого и второго вида не превышаетобщего количества ресурсов каждого типа.

Построим в плоскости X₁OX₂ область допустимых решений. Каждое неравенство системы (3.3.2) определяет в плоскости X₁OX₂ полуплоскость, лежащую выше или ниже прямой, определяемой соответствующим уравнением. Построим прямые (см. рис. 3.1)

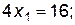
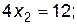
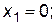
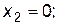
Рассмотрим точку с координатами х ₁ =0; х ₂ =0. Подставив их в первое неравенство, получаем 0 £ 12 – верно, следовательно, искомая полуплоскость лежит ниже прямой 2x₁ +2x₂ = 12; остальные полуплоскости находятся аналогичным образом.

Область OABCD – область допустимых решений задачи.

Для нахождения максимального значения Р проверим граничные. Точки из области решений.

Построим две линии уровня (рис. 3.1):

2x₁ + 3x₂ = 6;

2x₁ +3х₂=13.

Функция Р возрастает в направлении вектора-нормали 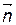= (2,3) следовательно, минимум находится в точке (0.0). Максимум определяем, передвигая нашу линию уровня в направлении вектора 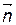параллельно самой себе до тех пор, пока хотя бы одна ее точка будет принадлежать области допустимых решений.

В данном случае это точка: х ₁= 4, х ₂= 2;

при этом P=2*4+3*2=14.

Таким образом, для получения максимальной прибыли в размере 14 усл. ед. надо продать 4 изделия первого вида и 2 изделия второго вида.

Рис. 3.1. Графический метод решения задачи ЛП

Изложенный выше графический метод применим для решения задач линейного программирования следующего вида:

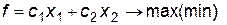(3.17)

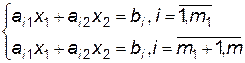(3.18)

Алгоритм решения ЗЛП графическим методом.

1) Записывают уравнения прямых, соответствующих ограничениям (3.3.4), и строят их на плоскости x₁ox_3.

2) Определяют области, в которых выполняются ограничения задачи. Для этого выбирают произвольную точку на плоскости х₁ох₂ и подставляют ее координаты в первую часть одного из неравенств. Если неравенство верно, то искомая полуплоскость находится с той же стороны от прямой, что и точка; в противном случае искомая полуплоскость лежит с противоположной стороны от прямой. Эти действия последовательно выполняются для всех неравенств (3.3.4).

3) Определяют область допустимых решений задачи как область пересечения т полуплоскостей, соответствующих т ограничениям задачи.

4) Определяют направление возрастания (убывания) целевой функции f. Это можно сделать двумя способами. Можно построить вектор-нормаль 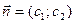, его направление показывает направление возрастания функции f, и противоположном направлении функция убывает. Можно просто построить две линии уровня функции f = K ₁; f = K ₂; (K ₁, K ₂ – произвольные константы, K ₁ 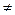K ₂), и по их расположению определить направление возрастания (убывания) функции.

5) Определяют граничную точку (точки) области допустимых решений, в которых целевая функция принимает максимальное или минимальное значение.

6) Вычисляют значения найденной точки, решая совместно уравнения, задающие прямые, на пересечении которых находится эта точка, или выявляя уравнение граничной прямой области допустимых решений, с которой совпадает линия уровня целевой функции.

Возможны следующие варианты областей допустимых решений (рис. 3.2):

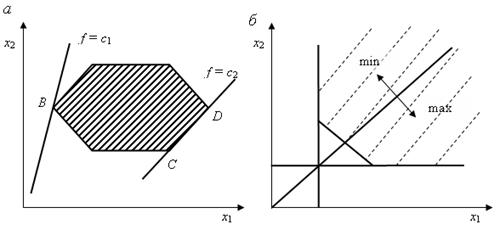
Рис. 3.2. Варианты областей. а – область допустимых решений
– замкнутое множество (многоугольник); б – область допустимых решений – открытое множество; в – область допустимых решений – пустое множество (система ограничений (3.18) несовместна);
г – область допустимых решений состоит из единственной точки А

На рис. 3.2 показаны варианты пересечения линии уровня целевой функции с областью допустимых решений. Может быть единственное решение – точка В, бесконечно много решений – отрезок CD (рис. 3.2, а), максимальным (минимальным) значением целевой функции может быть бесконечность (рис. 3.2, б). Область ограничений несовместимо (допустимых решений нет, рис. 3.2, в). И может быть только одна допустимая точка (рис. 3.2, г)

Дата добавления: 2015-04-24