Пример 3.4_2

Пример 3.4

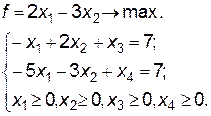
Базисные переменные: х_з,х₄.

Свободные переменные: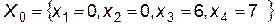

Симплекс-таблица имеет следующий вид (табл. 3.4):

Значение f можно увеличить, увеличивая значение переменной x₁,так как ей соответствует положительный коэффициент в формуле для f, соответственно, отрицательный коэффициент в последней строке симплекс-таблицы. Из системы ограничений видно, что при любом увеличении значения X₁можно подобрать значения х_з,х₄, при которых Будет выполняться система ограничений. Следовательно, функция f будет бесконечно возрастать и не будет ограниченной на области допустимых решений

Таблица 3.4

Базисные переменные	Коэффициенты при переменных	Свободные члены
х1	х2	х3	х4
х4 х3	-1 -5	-3
-f	-2

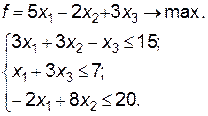
Запишем задачу в каноническом виде, вводя дополнительные переменные х₄, х₅, х_6.

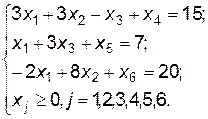
Начальное решение:

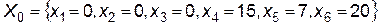
Функция Уже выражена через свободные переменные, поэтому можно перейти к составлению симплекс-таблицы
(табл. 3.5).

Таблица 3.5

Базисные переменные	Коэффициенты при переменных	Свободные члены
х1	х2	х3	х4	х5	х6
х4 х5 х6	-2		-1
-f	-5		-3

Ввод переменной в список базисных переменных означает, что ей приписывается отличное от 0 положительное значение, т. е. ее значение увеличивается. Из формулы для целевой функции видно, что увеличение значения х₂ приводит только к уменьшению f т. е. переменную х₂ бессмысленно вводить в список базисных переменных. Увеличение переменных х₁ и х₃ приводит к увеличению значения f при этом на большую величину значение изменяется с увеличением х_1, следовательно, переменная х₁ должна стать базисной переменной. Максимальное значение коэффициента при х₁ в формуле для f соответствует максимальному по абсолютной величине отрицательному элементу в последней строке симплекс-таблицы, следовательно, понятен выбор новой базисной переменной.

Для определения переменной, выводимой из списка оазисных переменных, надо в соответствии с алгоритмом симплекс-метода найти отношения элементов столбца свободных членов к элементам разрешающего столбца и среди них выбрать минимальное.

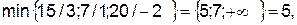
следовательно, из списка базисных переменных надо вывести х₄, стоящую в первой строке симплекс-таблицы, и разрешающий элемент a₁₁=3.

Поясним этот выбор. Если перейти от симплекс-таблицы к ограничениям, то это значит, что х₁надо выразить из первого уравнения через остальные переменные, включая х₄,и, подставив его во второе и третье уравнения, исключить оттуда х₄. Проделаем это ниже, а сейчас поясним, почему выбор пал именно на х₄.

Попробуем вывести из списка базисных другую переменную, например х₅. Для этого выразим х₁ через х₅ и остальные переменные из второго уравнения и подставим в остальные.

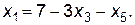
Подставив х₁ в первое уравнение, получим

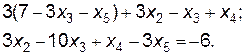
Подставив х₂ во второе уравнение, получим

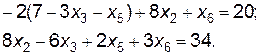
Окончательно получим

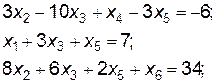
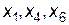– базисные переменные, поэтому решение имеет вид

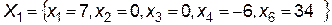
В этом решении x ₄ = -6, что противоречит условию задачи 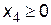следовательно, Х₁ не является допустимым решением, и, таким образом, переменную x ₅ нельзя вывести из списка базисных переменных.

Вывод из списка базисных переменных переменной х₆ означает, что x₁ надо выразить через х₆ из последнего уравнения исходной системы ограничений. Получившаяся при этом правая часть уравнения будет являться значением базисной переменной х₁ в новом решении.

Выразив х₁ через х₆, получим

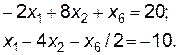
Следовательно, в новом решении х₁ = -10, что противоречит условию неотрицательности х₁, поэтому на шаге 4.2 пренебрегают делением на отрицательное число, полагая равным 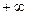результат от деления.

Дата добавления: 2015-04-24