Пример 13. (вторая теорема двойственности)

Теорема 9

(вторая теорема двойственности).

План 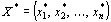задачи (43) – (45) и план задачи (46), (47) являются оптимальными планами этих задач тогда и только тогда, когда для любого 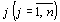выполняется равенство

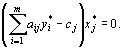
Геометрическая интерпретация двойственных задач. Если число переменных в прямой и двойственной задачах, образующих данную пару, равно двум, то, используя геометрическую интерпретацию задачи линейного программирования, можно легко найти решение данной пары задач. При этом имеет место один из следующих трех взаимно исключающих друг друга случаев: 1) обе задачи имеют планы; 2) планы имеет только одна задача; 3) для каждой задачи двойственной пары множество планов пусто.

Для задачи, состоящей в определении максимального значения функции 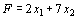при условиях

составить двойственную задачу и найти решение обеих задач.

Решение. Двойственной задачей по отношению к исходной является задача, состоящая в определении минимального значения функции 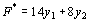при условиях

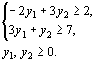
Как в исходной, так и в двойственной задаче число неизвестных равно двум. Следовательно, их решение можно найти, используя геометрическую интерпретацию задачи линейного программирования (рис. 7 и 8).

Как видно из рис. 8, максимальное значение целевая функция исходной задачи принимает в точке В. Следовательно, Х^*= (2, 6) является оптимальным планом, при котором 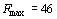. Минимальное значение целевая функция двойственной задачи принимает в точке Е (рис. 8). Значит, Y ^*=(1; 4) является оптимальным планом двойственной задачи, при котором 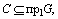Таким образом, значения целевых функций исходной и двойственной задач при их оптимальных планах равны между собой.

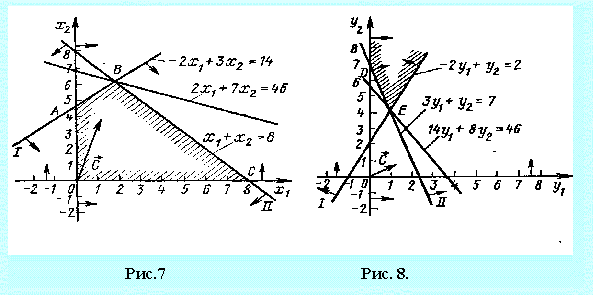
Из рис. 7 видно, что при всяком плане исходной задачи значение целевой функции не больше 46. Одновременно, как видно из рис. 8, значение целевой функции двойственной задачи при любом ее плане не меньше 46. Таким образом, при любом плане исходной задачи значение целевой функции не превосходит значения целевой функции двойственной задачи при ее произвольном плане.

Дата добавления: 2015-04-24