Общий вид транспортной задачи. В общем случае имеется m пунктов производства и n пунктов потребления

Транспортная задача

В общем случае имеется m пунктов производства и n пунктов потребления. Пункты производства пронумеруем числами от 1 до m. Номер пункта производства будем обозначать буквой i (таким образом, 1 £ i £ m). Пункты потребления пронумеруем числами от 1 до n. Номер пункта потребления будем обозначать буквой j (таким образом, 1£ j £ n). Рассмотрим некоторый период времени (например, месяц). Пусть a_i - объем производства за период времени в i-м пункте производства, b_i - количество продукции, требуемое за период времени в j-м пункте потребления. Пусть c_ij - стоимость перевозки единицы груза из i-го пункта производства в j-й пункт потребления.

Требуется определить план перевозок, удовлетворяющий условиям по пунктам производства и потребления и соответствующий наименьшим затратам на перевозки.

Для построения математической модели следует ввести переменные. Для каждой пары поставщик-потребитель, то есть для каждой пары (i,j) введем переменную х_ij - объем перевозки от пункта производства i к пункту потребления j.

Математическая модель транспортной задачи записывается следующим образом

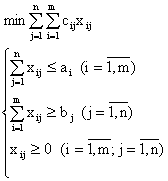
Целевая функция модели представляет собой общую стоимость всех перевозок. Она записана в виде двойной суммы. Внутренняя сумма соответствует пунктам производства, внешняя - пунктам потребления. Разумеется, эти знаки суммирования в целевой функции можно поменять местами. От перегруппировки слагаемых сумма не изменяется.

В модели указано, что целевую функцию следует минимизировать. Таким образом, модель предписывает искать план перевозок наименьшей общей стоимости.

В системе ограничений представлены три группы неравенств. В первой группе m неравенств, соответствующих пунктам производства. Каждое неравенство утверждает, что из соответствующего пункта не может быть вывезено больше, чем в нем имеется. Во второй группе n неравенств, соответствующих пунктам потребления. Каждое из них требует, чтобы в соответствующий пункт было привезено не меньше, чем требуется. В третьей группе m ´ n неравенств, обеспечивающих неотрицательность объема перевозок.

Представленная модель транспортной задачи с ограничениями-неравенствами называется открытой моделью. Задача разрешима в том и только в том случае, когда общий объем груза у поставщиков не меньше суммарной потребности потребителей, то есть когда выполнено неравенство:

.

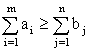Если выполнено обратное неравенство, то есть если

,

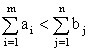то задача неразрешима, для нее не существует не только оптимального, но даже и допустимого плана.

Если общий объем груза у поставщиков в точности равен общей потребности потребителей, то есть если имеет место равенство:

,

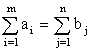то указанная выше открытая модель эквивалентна более простой закрытой модели, в которой основные неравенства заменены равенствами. Закрытая модель имеет следующий вид:

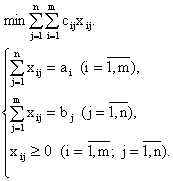
Дата добавления: 2015-04-24