Нелинейное программирование

Задача оптимизации в общем виде:

Минимизировать функцию:

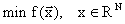
При ограничениях:

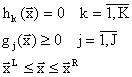
На вид функции ограничений не накладывается.

Можно выделить следующие типы методов решения задач нелинейного программирования:

1) Методы, основанные на прееобразовании задачи. Задача с ограничениями преобразуется в последовательность задач безусловной оптимизации.

2) Методы линеаризации. Нелинейные функции в постановке линеаризуются, то есть разлагаются в ряд Тейлора и оставляются только линейные члены, после чего решается последовательность задач линейного программирования.

3) Методы квадратичной аппроксимации. Аналогично, но в ряду Тейлора оставляются квадратичные члены. Получается последовательность задач квадратичного программирования.

4) Методы выбора напралений - модифицированные методы направлений безусловной оптимизации.

5) Методы прямого поиска. Дополнение изученных методов проверками на попадание в условия.

Методы преобразования задач

Пусть 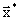является решением задачи оптимизации в общем виде. Возьмём некоторое начальное приближение 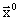, возможно недопустимое (не удовлетворяющее ограничениям), тогда пространстве R^N строится последовательность векторов 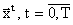. Последовательность заканчивается 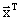, которое даёт некоторое приближение к решению. В качестве 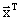на каждой итерации берутся стационарные точки так называемой штрафной функции (ШФ). Она является вспомогательной задачей условной оптимизации. С помощью ШФ исходная задача сводится к последовательности задач безусловной оптимизации.

ШФ - это функция вида:

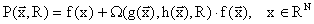
W - штраф, R - штрафной параметр.

R меняется на каждой итерации и фактически используется набор штрафных параметров R^(t). W имеет различный вид для равенств и неравенств. При построении W должны выполняться следующие условия:

1) Решения подзадач безусловной оптимизации должны стремиться к решению исходной задачи, то есть:

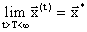
2) Сложность задачи оптимизации функции 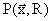должна быть хотя бы того же порядка, что и для функции .

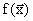3) Правило пересчёта штрафного параметра на каждой итерации должно быть достаточно простым.

Основные типы штрафов

Штрафы, учитывающие ограничения-равенства.

Для учёта ограничений равенств всегда используется квадратичный штраф.

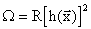
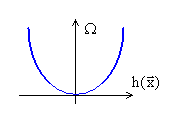
Этот штраф препятсятвует отклонению 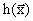от 0 как в положительную, так и в отрицательную стороны.

При этом R начинается с 0 или наибольшего положительного числа и возрастает от итерации к итерации.

Если есть несколько ограничений равенств, то:

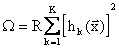
Штрафы, учитывающие ограничения-неравенства.

1) Бесконечный барьер.

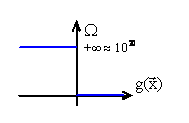
Этот штраф принимает бесконечно большое значение в недопустимых точках и 0 в допустимых.

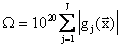
2) Логарифмический штраф.

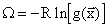
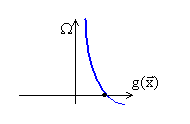
R начинается с большого положительного числа и стремится к нулю.

Штраф положителен на всех 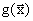на [0,1] и отрицптелен для 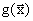> 1.

3) Штраф, задаваемый обратной функцией.

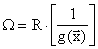
R начинается с большого положительного числа и стремится к нулю.

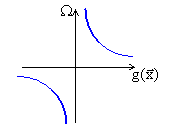
В недопустимых точках штраф имеет отрицательное значение, а в допустимых - положительное.

4) Штраф типа квадрата срезки.

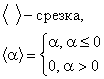
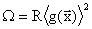
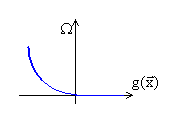
R начинается с 0 и растёт от итерации к итерации. В допустимых точках штраф равен нулю.

Дата добавления: 2015-04-24