Вопрос 21.Ортогональная, ортонормированная матрица, неквадратная матрица с ортогональными (ортонормированными) столбцами

2)

Если линейная комбинация может представлять собой нулевой вектор тогда, когда среди чисел есть хотя бы одно, отличное от нуля, то система векторов 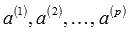называется линейно зависимой.

Если линейная комбинация представляет собой нулевой вектор только тогда, когда все числа равны нулю, то система векторов 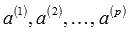называется линейно независимой.

3) Размерностью2) ненулевого векторного пространства называется мощность его базиса. Для нулевого векторного пространства полагают, что его размерность равна нулю. Размерность векторного пространства над полем обозначается через .

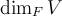Определение 3. Говорят, что пространство конечномерно если или базис состоит из конечного числа векторов. В противном случае говорят, что бесконечномерно

4) Когда мы разбирали понятия n-мерного вектора и вводили операции над векторами, то выяснили, что множество всех n-мерных векторов порождает линейное пространство. В этой статье мы поговорим о важнейших связанных понятиях – о размерности и базисе векторного пространства. Также рассмотрим теорему о разложении произвольного вектора по базису и связь между различными базисами n-мерного пространства. Подробно разберем решения характерных примеров.
Размерностью векторного пространства называется число, равное максимальному количеству линейно независимых векторов в этом пространстве.

Базис векторного пространства – это упорядоченная совокупность линейно независимых векторов этого пространства, число которых равно размерности пространства.

5) Скалярным произведением векторов а и б называется произведение их длин на косинус угла между ними:
Совершенно аналогично, как в планиметрии, доказываются следующие утверждения:

Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.

Скалярный квадрат вектора, то есть скалярное произведение его самого на себя, равно квадрату его длины.

Скалярное произведение двух векторов и заданных своими координатами, может быть вычислено по формуле
Перечислим основные свойства скалярного произведения, которые также доказываются аналогично планиметрическим.

Для любых векторов а б и с и любого числа λ справедливы равенства:

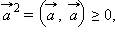
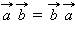
7) Базис любого конечномерного подпространства S в унитарном или евклидовом пространстве Rявляется невырожденным рядом векторов и потому согласно теореме 2 предыдущего параграфа может быть проортогонализирован и пронормирован. Таким образом, в любом конечномерном подпространстве S (и, в частности, во всем пространстве R, если оно конечномерно) существует ортонормированный базис. В ортонормированном базисе координата вектора равна скалярному произведению его на соответствующий базисный орт
10) Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. В математике рассматривается множество различных типов и видов матриц. Таковы, например, единичная, симметричная, кососимметричная, верхнетреугольная (нижнетреугольная) и т. п. матрицы.
11) Определителем матрицы второго порядка, или определителем второго порядка, называется число, которое вычисляется по формуле: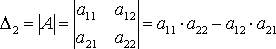

Определителем матрицы третьего порядка, или определителем третьего порядка, называется число, которое вычисляется по формуле:
След матрицы — это сумма элементов главной диагонали матрицы
12) Минор k -го порядка матрицы (от лат. minor – меньший) – определитель матрицы, составленный из элементов данной матрицы, стоящих на пересечении произвольно выделенных ее k строк и k столбцов с сохранением их порядка, т.е. минор k-го порядка есть определитель квадратной матрицы размера k x k. Минорами 1-го порядка являются элементы матрицы. Если номера строк, в которых расположен минор, совпадают с номерами столбцов, то он называется главным минором. Базисный минор матрицы – отличный от нуля минор k-го порядка этой матрицы такой, что все содержащие его миноры (k+1)-го порядка равны нулю, или же минор (k+1)-го порядка не существует. Порядок любого базисного минора матрицы совпадает с рангом матрицы, причем каждый столбец (строка) матрицы есть линейная комбинация линейно независимых столбцов (строк), в которых расположен базисный минор.

В квадратной матрице n-го порядка дополнительным минором к минору k-го порядка называется определитель (n-k)-го порядка, полученный из данной матрицы вычеркиванием тех k столбцов и строк, в которых расположен минор k-го порядка.
13) Рангом матрицы называется наибольший из порядков миноров матрицы, отличных от нуля. Ранг нулевой матрицы считается равным нулю. Ранг матрицы размера m*n называют полным, если .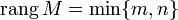

14) Транспонированная матрица — матрица , полученная из исходной матрицы A заменой строк на столбцы.

Формально, транспонированная матрица для матрицы A размеров m*n — матрица A^T размеров m*n, определённая как A^T[i, j] = A[j, i].

При транспонировании матрицы ее ранг не меняется.
Свойства

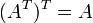
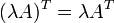
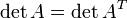
15) Симметрическая матрица, квадратная матрица S = llsikll, в которой любые два элемента, симметрично расположенные относительно главной диагонали, равны между собой: sik = ski (i, k = 1,2,..., n). С. м. часто рассматривается как матрица коэффициентов некоторой квадратичной формы;
16) Суммой двух прямоугольных матриц A=a(ik) и B=b(ik) одинаковых размеров m*n называется матрица C=c(ik) тех же размеров, элементы которой равны суммам соответствующих элементов данной матрицы: C=A+B

Операция нахождения суммы данных матриц называется сложением матриц.
17) Произведением матрицы А на число l называется матрица В, которая получается из матрицы А умножением всех ее элементов на l
18) Произведением двух прямоугольных матриц A иB

называется матрица C у которой элемент с(iJ), стоящий на пересеченииi -й строки иj -го столбца, равен «произведению» i-й строки первой матрицы A на j-й столбец второй матрицы B.З аметим, что операция умножения двух прямоугольных матриц выполнима лишь в том случае, когда число столбцов в первом сомножителе равно числу строк во втором. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка. Легко проверяется сочетательное свойство умножения матриц, а также распределительное свойство умножения относительно сложения:
1) A(BC)=(AB)C
2)(A+B)C=AB+BC
3)A(B+C)=
19) Векторно-скалярное произведение трех векторов a b и c или смешанное их произведение вычисляется по формуле a*(b*c)
Абсолютная величина векторно-скалярного произведения равна объему параллелепипеда, построенного на векторах a, b и c. Объем пирамиды, построенной на векторах a, b и c, получим по формуле 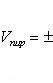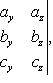причем знак перед определителем должен быть выбран так, чтобы объем V был положительным (предполагается, что векторы a, b и c не лежат в одной плоскости)
20) Если существуют квадратные матрицы Х и А одного порядка, удовлетворяющие условию:

XA = AX = E,

где Е - единичная матрица того же самого порядка, что и матрица А, то матрица Х называется обратной к матрице А и обозначается А-1. Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну.

Ортогональная матрица — квадратная матрица A с вещественными элементами, результат умножения которой на A^T равен единичной матрице:^[1]

или, что эквивалентно, её обратная матрица равна транспонированной матрице:

Матрица, столбцы и строки которой образуют системы ортонормированных векторов. Другими словами, скалярное произведение строки на саму себя равно 1, а на любую другую строку — 0. Так же и для столбцов.

Дата добавления: 2015-04-24