Характер стоксова обтекания сферы потоком вязкой жидкости при малых скоростях

36.

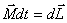
Это выражение носит название основного уравнения динамики вращательного движения и формулируется следующим образом: изменение момента количества движения твердого тела 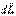, равно импульсу момента 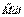всех внешних сил, действующих на это тело.

Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:

,

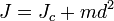где 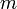— полная масса тела.

37. Теоре́ма Гю́йгенса — Ште́йнера, или просто теорема Штейнера: момент инерции тела 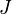относительно произвольной оси равен сумме момента инерции этого тела 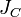относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела 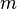на квадрат расстояния 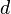между осями: 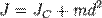где

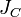— известный момент инерции относительно оси, проходящей через центр масс тела,

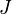— искомый момент инерции относительно параллельной оси,

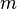— масса тела,

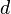— расстояние между указанными осями.

38. Уравнение состояния газа Ван-дер-Ваальса — уравнение, связывающее основные термодинамические величины в модели газа Ван-дер-Ваальса.

Хотя модель идеального газа хорошо описывает поведение реальных газов при низких давлениях и высоких температурах, в других условиях её соответствие сопытом гораздо хуже. В частности, это проявляется в том, что реальные газы могут быть переведены в жидкое и даже в твёрдое состояние, а идеальные — не могут.

Для более точного описания поведения реальных газов при низких температурах была создана модель газа Ван-дер-Ваальса, учитывающая силы межмолекулярного взаимодействия. В этой модели внутренняя

энергия U становится функцией не только температуры, но и объёма.

Для одного моля газа Ван-дер-Ваальса оно имеет вид: (p+a/V_m ²)(V_m — b) = RT

Где p — давление,

V — молярный объём,

T— абсолютная температура,

R— универсальная газовая постоянная.

a и b — экспериментальные константы, учитывающие отклонение свойств реального газа от свойств идеального газа.

39. 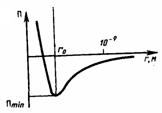Элементарная работа dA силы F при увеличении расстояния между молекулами на dr совершается за счет уменьшения взаимной потенциальной энергии молекул, т. е. 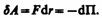Из анализа качественной зависимости потенциальной энергии взаимодействия молекул от расстояния между ними (рис.) следует, что если молекулы находятся друг от друга на расстоянии, на котором межмолекулярные силы взаимодействия не действуют, то П=0. При постепенном сближении молекул между, ними появляются силы притяжения (F<0), которые совершают положительную работу (dA=Fdr > 0). Тогда, согласно формуле, потенциальная энергия взаимодействия уменьшается, достигая минимума при r= r0. При r < r0 с уменьшением r силы отталкивания (F>0) резко возрастают и совершаемая против них работа отрицательна (dA=Fdr<0). Потенциальная энергия начинает тоже резко возрастать и становится положительной. Из данной потенциальной кривой следует, что система из двух взаимодействующих молекул в состоянии устойчивого равновесия (r = r0) обладает минимальной потенциальной энергией.

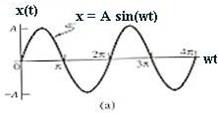
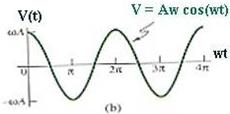
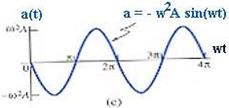
40. Гармоническое колебание — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону

Кинематическое уравнение гармонических колебаний имеет вид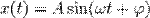

или ,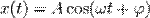

где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия; ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд — полная фаза колебаний, 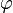— начальная фаза колебаний.

Обобщенное гармоническое колебание в дифференциальном виде

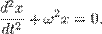
(Любое нетривиальное^[1] решение этого дифференциального уравнения — есть гармоническое колебание с циклической частотой )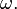

Гармонические колебания выделяются из всех остальных видов колебаний по следующим причинам:

· Очень часто^[2] малые колебания, как свободные, так и вынужденные, которые происходят в реальных системах, можно считать имеющими форму гармонических колебаний или очень близкую к ней.

· Широкий класс периодических функций может быть разложен на сумму тригонометрических компонентов. Другими словами, любое колебание может быть представлено как сумма гармонических колебаний.

· Для широкого класса систем откликом на гармоническое воздействие является гармоническое колебание (свойство линейности), при этом связь воздействия и отклика является устойчивой характеристикой системы. С учётом предыдущего свойства это позволяет исследовать прохождение колебаний произвольной формы через системы.

42. Идеальный газ — это упрощенная модель реальных газов. В этой модели не учитываются объем молекул и силы взаимодействия между ними. Между тем молекулы реальных газов занимают определенный объем и взаимодействуют между собой. При больших давлениях и низких температурах становится заметным влияние собственных объемов молекул и сил взаимодействия между ними. При этих условиях уравнение Клапейрона—Менделеева и законы Бойля—Мариотта, Гей-Люссака, Шарля непригодны для описания состояния реальных газов.

Молекулы не только отталкиваются при соударениях, но еще и притягиваются друг к другу сравнительно слабыми силами на расстояниях, сравнимых с размерами молекул.

Запишем уравнение Клапейрона—Менделеева для одного моля идеального газа (m = M)

pVM = RT

, где V _M — молярный объем газа.

Учет собственного объема молекул приводит к тому, что фактический свободный объем, в котором могут двигаться молекулы реального газа, будет не V _M, a (V _M - b), где постоянная b равна приблизительно учетверенному собственному объему молекул.

Действие сил притяжения между молекулами реального газа приводит к появлению дополнительного давления на газ. При приближении некоторой молекулы к стенке сосуда все остальные молекулы оказываются по одну сторону от нее и равнодействующая сил притяжения, действующих на эту молекулу, оказывается направленной от стенки сосуда внутрь газа. Это приводит к тому, что уменьшается импульс, передаваемый молекулой стенке сосуда. В результате давление газа p на стенки сосуда уменьшается по сравнению с тем p _id, каким оно было бы в отсутствие сил притяжения

p = pid − p ′⇒ pid = p + p ′

Как показывают расчеты, это дополнительное давление обратно пропорционально квадрату объема газа, т.е.

p ′= aV 2 M,

где а — постоянная.

Вводя эти поправки, получим уравнение Ван-дер-Ваальса для одного моля газа (уравнение состояния реальных газов)

(p + aV 2 M)(VM − b)= RT.

Если газ произвольной массы m занимает объем V, то его молярный объем VM = Vν, где количество газа ν = mM. Подставив значение молярного объема, получим уравнение Ван-дер-Ваальса для произвольного числа ν молей газа:

(p + m 2 M 2 aV 2)(V − mMb)= mMRT.

Постоянные для каждого газа поправки a и b находят экспериментально.

Так как молекулы идеального газа не имеют объема и не взаимодействуют между собой, то идеальный газ при любых изменениях его параметров остается газом.

Совсем иначе ведут себя реальные газы. Чтобы убедиться в этом, исследуемый газ помещают в прозрачный цилиндр с подвижным поршнем (рис. 1), который помещают в термостат.

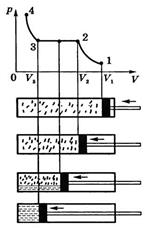
Рис. 1

При медленном сжатии газа температура его не изменяется (процесс изотермический) и давление газа увеличивается в соответствии с законом Бойля—Мариотта. На графике эта стадия опыта изображена кривой 1-2. Но, начиная с некоторого объема, дальнейшее уменьшение объема газа уже не приводит к увеличению давления, а на стенках цилиндра появляются капельки жидкости. При этом находящиеся одновременно газ и жидкость имеют одинаковую температуру и находятся под одинаковым давлением, т.е. находятся в термодинамическом равновесии.

Газ, находящийся в термодинамическом равновесии со своей жидкостью, называется насыщенным паром.

Таким образом, участок изотермы 2-3 соответствует насыщенному пару над жидкостью (двухфазная среда). Когда весь газ превратится в жидкость, дальнейшее уменьшение объема приводит к резкому возрастанию давления (участок кривой 3-4), поскольку молекулы в жидкости упакованы достаточно плотно и ее сжимаемость мала. Вся кривая 1-2-3-4 называется изотермой реального газа.

Таким образом, изотермы реального газа заметно отличаются от изотерм идеального газа наличием у них горизонтальных участков, соответствующих области существования двухфазной системы.

Следовательно, основное отличие реальных газов от идеального состоит в том, что реальный газ может быть превращен в жидкость.

41.

42.Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.

Реальный газ — газ, который не описывается уравнением состояния идеального газа Клапейрона — Менделеева.

Зависимости между его параметрами показывают, что молекулы в реальном газе взаимодействуют между собой и занимают определенный объем. Состояние реального газа часто на практике описывается обобщенным уравнением Менделеева — Клапейрона: PV = n RT

где n – число молей газа;

P – давление газа (например, в атм;

V – объем газа (в литрах);

T – температура газа (в кельвинах);

R – газовая постоянная (0,0821 л· атм /моль·K).

Молекулы идеального они не сталкиваются друг с другом. а в реальном газе они движутся сталкиваясь. идеальный газ поэтому легче рассчитывать. но в реале идеального газа не существует.

43. Тепловая машина состоит из нагревателя, рабочего тела и охладителя рабочего тела. Охладителем, в конечном счете, служит окружающая среда. Тепловая машина работает по принципу замкнутого цикла, совершая круговой процесс. В ходе прямого цикла рабочее тело, например, пар, получив от нагревателя количество тепла Q₁, расширяется от объема V₁ до объема V₃. Согласно первому закону термодинамики, это тепло расходуется на нагревание рабочего тела и на совершение механической работы

Q₁ = E₂ ‑ E₁ + A₁₃, (2.52)

где E₂ ‑ E₁ — изменение внутренней энергии рабочего тела при переходе из состояния 1 в состояние 3. При обратном цикле над газом производится работа: газ сжимается и передает охладителю количество тепла

‑ Q₂ = E₁ ‑ E₂ + A₃₁ (2.53)

Складывая оба уравнения, получим Q₁ ‑ Q₂ = A₁₃ + A₃₁ = A, где А — полная работа, совершенная машиной за один цикл.

Отношение полезной работы, совершенной машиной, к количеству полученного тепла составляет КПД тепловой машины

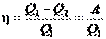. (2.54)

Понятно, что КПД машины всегда меньше единицы, поскольку не все количество полученного тепла переходит в полезную работу.

В качестве рабочего тела в цикле Карно рассматривается идеальный газ. Цикл Карно состоит из последовательных расширения и сжатия газа, причем каждый из процессов совершается сначала изотермически, а затем адиабатически. При прямом цикле тело по-прежнему сначала получает тепло, а затем отдает его. Достоинство цикла Карно состоит в том, что все процессы обратимы, и, следовательно, КПД такой машины будет максимальным.

Пусть газ расширяется изотермически, переходя из состояния 1 в состояние 2. При изотермическом процессе внутренняя энергия газа не изменяется, и количество полученного тепла Q₁ равно работе А₁₂. По формуле (2.38):

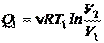. (2.55)

На участке 2-3 газ расширяется адиабатически. На участке 3‑4 он сжимается опять изотермически, для чего охладителю должно быть отдано тепло Q₂. Работа на участке 3‑4 равна ‑ Q₂, причем

. (2.56)

Наконец, на участке 4‑1 газ адиабатически сжимается, возвращаясь к исходному состоянию. Воспользуемся уравнением адиабаты (2.42), заменив в нем, согласно уравнению состояния PV, на ν· RT. Уравнение адиабаты принимает вид:

TV ^γ‑1 = const. (2.57)

Для процессов 2‑3 и 4‑1 цикла Карно отсюда следует:

.

Разделив первое уравнение на второе, получим V ₂ /V ₁ = V ₃ /V ₄. После подстановки этого выражения в (2.56) найдем:

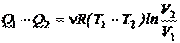. (2.58)

Подставляя (2.58) в формулу (2.54), получим выражение для КПД цикла Карно:

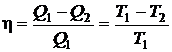. (2.59)

Из формулы (2.59) следует, что КПД тепловой машины определяется только разностью температур нагревателя и холодильника. КПД не зависит ни от свойств рабочего тела, используемого в машине, ни от свойств самой машины. Полученный результат показывает, что при T₁ = T₂ КПД машины равен нулю, т. е. машина не совершает работы. Работа максимальна (η = 1) при T₂ = 0. Таким образом, машина тем выгоднее, чем ниже температура охладителя.

44 Кинетическая энергия системы, совершающей гармонические колебания, равна:

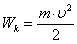(43)

где скорость изменяется по гармоническому закону:

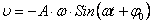(44)

После подстановки, имеем:

Вывод: 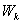физической системы совершает гармонические колебания с круговой частотой 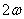, а величина ее периодически изменяется от 0 до .

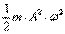Гармоническое колебание — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид

или

,

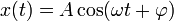где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия; ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд; — полная фаза колебаний, 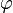— начальная фаза колебаний.

Обобщенное гармоническое колебание в дифференциальном виде

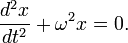
45Рассмотрим небольшой шарик массой 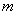, к которому прикреплена горизонтально расположенная пружина. Другой ее конец закреплен (рис. 2). Направим ось 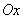вдоль оси пружины, за начало координат примем положение равновесия шарика. Если немного сместить шарик вдоль оси, то возникнет упругая сила 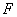, стремящаяся вернуть его в положение равновесия. По закону Гука, эта сила пропорциональна смещению 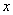, т.е. 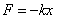( 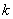- положительная константа, характеризующая упругие свойства пружины, знак «минус» ставится потому, что сила восстанавливающая). Согласно второму закону Ньютона, сила, действующая на тело массой 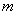, равна произведению массы на ускорение :

.

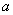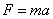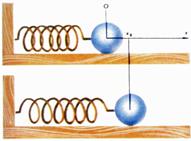
Рис. 2

Если же 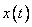- положение шарика в момент времени 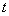, то его ускорение выражается второй производной 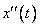. Таким образом, движение шарика под действием упругих сил можно выразить дифференциальным уравнением

,

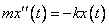которое чаще записывается в ви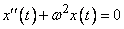де

, где .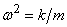

Это уравнение называется дифференциальным уравнением гармонических колебаний. Можно доказать, что любое его решение может быть записано в виде

,

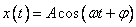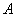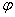здесь и - произвольные постоянные. Движения, характеризуемые таким уравнением, называются гармоническими колебаниями. Они представляют собой периодическое движение (рис. 3) с периодом 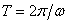; величина 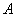называется амплитудой колебания.

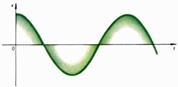
Рис. 3

Очевидно, что дифференциальное уравнение 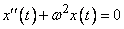не вполне определяет движение шарика. Оно зависит от того, на какую величину 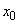шарик был смещен в момент времени 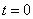и с какой скоростью он отпущен, т.е. зависит от начальных данных. Если, например, скорость была нулевой, то движение шарика будет подчиняться закону

.

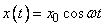Полученное нами выше дифференциальное уравнение есть математическая форма записи (математическая модель) закона движения под действием только силы упругости. Если рассмотреть движение шарика в среде, оказывающей сопротивление, и предположить, что кроме сил упругости на шарик действует сила сопротивления, пропорциональная скорости движения, то дифференциальное уравнение такого движения будет иметь вид:

.

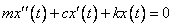Решения этого уравнения уже не являются периодическими функциями, а представляют собой колебания с изменяющейся амплитудой, так называемые затухающие колебания (рис. 4).

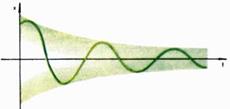
Рис. 4

Если неизвестная функция зависит от одной переменной, то дифференциальное уравнение называется обыкновенным; таковы рассмотренные выше уравнения. Порядком дифференциального уравнения называется порядок старшей производной, входящей в него. Как видим, уравнение 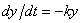первого порядка, уравнение 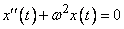- второго порядка.

46 Цикл Карно.

1. Состоит из двух изотерм и двух адиабат.

2. Рабочее тело – идеальный газ.

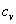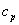3. Величины и - постоянные.

1-2, 3-4 – изотермические процессы.

2-3, 4-1 - , .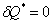

.

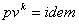Подвод теплоты от горячего источника производится на изотерме 1-2 при температуре Т₁, при этом рабочее тело - идеальный газ расширяется и совершается полезная работа. В процессе дальнейшего расширения по адиабате 2-3 до температуры Т₂ также совершается полезная работа. Для осуществления последующих процессов - сжатия 3-4 по изотерме Т₂ с отводом теплоты к холодному источнику и адиабатного сжатия 4-1 до начальной температуры Т₁ работа затрачивается.

Термодинамический коэффициент полезного действия 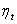определяется температурами холодильника и нагревателя.

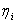- индикаторный КПД.

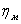- механический КПД.

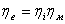- эффективный КПД.

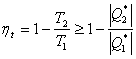
47. Круговой процесс – процесс, который характеризуется возвратом в исходное состояние системы (рабочего тела).

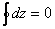, где 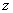- любая из характеристик процесса, таких как давление, объём, температура, энергия, энтальпия и энтропия.

Циклы – периодически повторяющиеся в тепловых машинах круговые процессы.

Если круговой процесс идёт по часовой стрелке это означает, что по верхней дуге тепло подводится, а по нижней отводится. Такой процесс называется прямым и реа 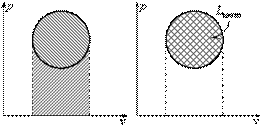лизуется в тепловых машинах.

Если круговой процесс идёт против часовой стрелки это означает, что по нижней дуге идёт подвод тепла, а по верхней дуге идёт отвод тепла. Такой процесс называется обратным и реализуется в холодильных машинах.

Различают три вида циклов тепловых машин: реальные, обратимые и термодинамические.

В реальных циклах тепловых машин имеют место внешняя и внутренняя необратимости.

Внешняя необратимость определяется конечной разностью температур между рабочим телом и источниками теплоты. Этим объясняется то, что реальный цикл теплового двигателя располагается внутри границ температур внешних источников, а реальный цикл холодильной машины - вне границ температур внешних источников.

Внутренняя необратимость обусловлена потерями энергии, связанными с трением, завихрениями и т.д. в процессах цикла.

В обратимых циклах тепловых машин отсутствует внешняя и внутренняя необратимости.

В термодинамических циклах тепловых машин, в отличие от реальных и обратимых циклов, рассматривается не вся система, включающая внешние источники теплоты, а только рабочее тело. При этом в процессах термодинамических циклов отсутствует внутренняя необратимость, то есть все процессы таких циклов являются обратимыми.

Эффективность любого реального теплового двигателя определяется коэффициентом полезного действия (КПД).

Коэффициент полезного действия реальных циклов тепловых двигателей численно равен отношению полученной работы к подведенному извне количеству теплоты

.

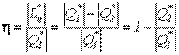Для обратимого цикла теплового двигателя КПД определяется следующим образом:

h _обр = .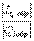

Термический коэффициент полезного действия термодинамического цикла теплового двигателя находится из соотношения

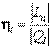
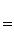
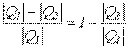Эффективность циклов холодильных машин оценивается холодильным коэффициентом (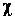). Холодильный коэффициент численно равен отношению количества теплоты, отводимой от холодного источника, к затраченной работе.

Для реального цикла холодильной машины холодильный коэффициент определяется соотношением

,

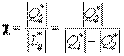для обратимого цикла холодильной машины – из зависимости

,

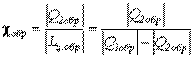а для термодинамического цикла холодильной машины – по соотношению

.

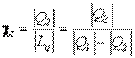48 Механика сплошных сред изучает движение и равновесие газов, жидкостей и деформируемых твёрдых тел. Моделью реальных тел в М. с. с. является сплошная среда (СС); в такой среде все характеристики вещества являются непрерывными функциями пространст-венных координат и времени. При деформации СС её частицы (их размеры значительно больше размеров атомов и молекул, но значительно меньше характерных размеров исследуемой теоретически или экспериментально системы) механически взаимодействуют между собой и с окружающими среду границами. Наряду с механическими взаимодействиями в некоторых случаях существенны взаимодействия немеханической природы — тепловое, химическое и др., а также взаимодействие среды с заполняющим пространство полем — электромагнитным, гравитационным, которое тоже может рассматриваться как особого рода СС.

Уравнение Бернулли считается одним из основных законов гидромеханики, он устанавливает связь между давлением в потоке жидкости и скоростью его движения в гидравлических системах: с увеличением скорости движения потока давление в нем должно падать. С его помощью объясняются многие гидродинамические эффекты.

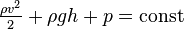
Здесь 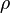— плотность жидкости,

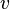— скорость потока,

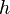— высота, на которой находится рассматриваемый элемент жидкости,

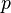— давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,

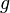— ускорение свободного падения.

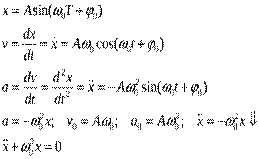
50. Процесс, протекающий без теплообмена с окружающей средой, называется адиабатным.

Первое начало термодинамики для него будет иметь вид: dQ = 0. С=0.

Тогда dU + dA = 0 или

dA = - dU = - cvdT, т.е. при адиабатном

процессе работа расширения совершается газом за счет уменьшения внутренней энергии.

Найдем уравнение, связывающее параметры идеального газа при адиабатном процессе. 1 начало термодинамики можем записать так: cvdT + pdV= 0.

Теперь выразим р через V и Т в соответ-ствии с уравнением состояния Идеального газа для 1 моля рV = RT:

СvdT + RT*dV/V=0.

Преобразуем полученное выражение следующим образом:

dT/Т+R/c_v*dV/V = 0

Последнее соотношение можно записать в виде d(lnT + R/c_v lnV) = 0.

Откуда следует, что при адиабатном процессе lnT + R/c_v lnV = const.

Преобразуем соотношение

R/c_v=(c_p-cv)/c_v= γ −1,где γ = c_p/c_v.

Пропотенцировав полученное ранее выражение, придем к уравнению

T V ^{γ −1} = const.

Полученное соотношение представляет собой уравнение адиабаты идеального газа в переменных T и V. От этого уравнения легко перейти(Т=pV/R) к уравнению pV ^γ = сonst.

Это соотношение есть уравнение адиабаты идеального газа в переменных p и V. Его называют также уравнением Пуассона. γ называют показателем адиабаты.

51. Уравнение состояния идеального газа (Менделеева-Клапейрона) 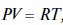Подставляя температуру Т из (1.22), учитывая, что R = const, получим уравнение адиабаты в переменных Р и V, называемое также уравнением Пуассона:

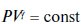(1.27)

Кроме того, так как удельный объем V связан с плотностью газа обратной пропорциональностью V = 1/ν, уравнение (1.28) можно привести к виду:

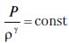,или ,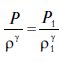

где Р₁ и ρ₁ давление и плотность газа в произвольном начальном состоянии.

52. Формула Стокса, являясь одной из ключевых формул векторного анализа, находит широкое применение в механике сплошных сред (особенно гидро- и аэродинамике), электродинамике и т.д.

Предельную скорость u _пр падения шарика малых размеров в вязкой жидкости находят по формуле

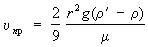
где r’ и r — плотность жидкости и вещества шарика, g — ускорение свободного падения.

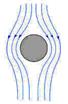
Сила сопротивления F, действующая со стороны потока жидкости на медленно движущееся в ней со скоростью u тело сферической формы радиуса R, определяется поформуле Стокса:

F = 6·p·h· R · u.

Данная формула справедлива при Re <<1 (Re = u · R ·r/ h; где r - плотность жидкости).

53. Сложение взаимно перпендикулярных колебаний.

Пусть 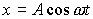и 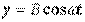, тогда траекторией будет прямая линия, :

.

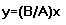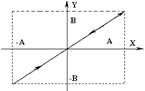
Пр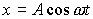и и 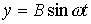, траекторией будет эллипс, (x²/A²)+(y²/B²)=1.:

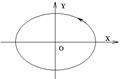
При разных частотах складывающихся колебаний результирующие траектории будут иметь более сложный вид.

Найдем результат сложения двух гармонических колебаний одинаковой частоты ω, которые происходят во взаимно перпендикулярных направлениях вдоль осей х и у. Начало отсчета для простоты выберем так, чтобы начальная фаза первого колебания была равна нулю, и запишем это в виде

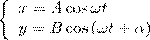(1)

где α — разность фаз обоих колебаний, А и В равны амплитудам складываемых колебаний. Уравнение траектории результирующего колебания определим исключением из формул (1) времени t. Записывая складываемые колебания как


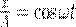
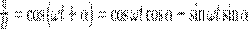
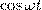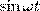и заменяя во втором уравнении на и на 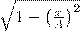, найдем после несложных преобразований уравнение эллипса, у которого оси ориентированы произвольно относительно координатных осей:

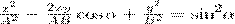
Постоянные	1-й закон термодинамики	Физический Смысл
Процесс Изотермическое сжатие
m=const M=const T=const pV=const	A=-Q	Изотермический процесс не может происходить без теплопередачи. Вся работа внешних сил выделяется в виде тепла.
Процесс Изохорное нагревание
m=const M=const V=const	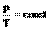A=0 Q= DU	Все количество теплоты, переданное системе, расходуется на увеличение ее внутренней энергии.
ПроцессИзохорное охлаждение
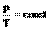
m=const M=const V=const	A=0 Q= DU<0	Система уменьшает свою внутреннюю энергию, отдавая теплоокружающим телам.
Процесс Изобарное расширение (нагревание)
m=const M=const p=const	Q=DU+A' DU=Q-А'>0	Количество теплоты, переданное системе, превышает совершенную механическую работу. Часть тепла расходуется на совершение работы, а часть – на увеличениевнутр. энергии.
Процесс Изобарное сжатие (охлаждение)
m=const M=const p=const	DU=Q+A<0 Q<0	Количество теплоты, отдаваемое системой, превышает работу внешних сил. Часть тепла система отдает за счет уменьшениявнутр. энергии.
Процесс Адиабатное Расширение
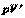m=const M=const =const	Q=0 A' > 0 DU=-A' < 0 A'=-DU	Система совершает механическую работу только за счет уменьшения своей внутренней энергии.
Процесс Адиабатное сжатие
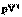m=const M=const =const	Q=0 A>0 DU=A	Внутренняя энергия системы увеличивается за счет работы внешних сил.

55. Теплоёмкость.

теплоёмкость –количество тепла,которое надо сообщить еденице массы,количества или объема вещества,чтобы его температура повысилась на 1 градус.

Истинная теплоемкость: 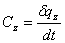, где 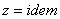- какой-то процесс. 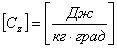. При изохорном процессе 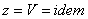, следовательно, получаем изохорную теплоёмкость - 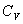. При изобарном процессе 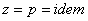, следовательно, получаем изобарную теплоёмкость .

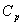Объёмная теплоёмкость

:

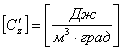· Объемная изобарная теплоёмкость - .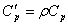

· Объёмная изохорная теплоёмкость - .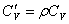

Молярная теплоёмкость

:

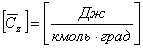·Молярная изобарная теплоёмкость - .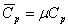

·Молярная изохорная теплоёмкость - .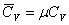

Средняя теплоёмкость

.

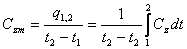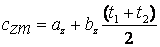-первая сред.теплоемкость-численно равна истинной теплоемкоти при среднеарифм.температуре процесса.

56.

57. Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение в одной вертикальной плоскости под действием силы тяжести.

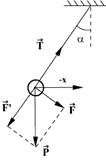
Таким маятником можно считать тяжелый шар массой m, подвешенный на тонкой нити, длина l которой намного больше размеров шара. Если его отклонить на угол α (рис.) от вертикальной линии, то под влиянием силы F – одной из составляющих веса Р он будет совершать колебания. Другая составляющая 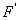, направленная вдоль нити, не учитывается, т.к. уравновешивается силой натяжения нити. При малых углах смещения 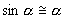и, тогда координату х можно отсчитывать по горизонтальному направлению. Из рис. видно, что составляющая веса, перпендикулярная нити, равна

Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α

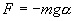
Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения Момент силы относительно точки О:

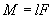, и момент инерции: M = FL.
Момент инерции J в данном случае
Угловое ускорение: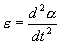

С учетом этих величин имеем:

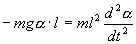
Или

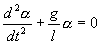
Его решение ,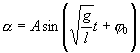

где 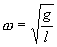и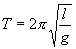

Как видим, период колебаний математического маятника зависит от его длины и ускорения силы тяжести и не зависит от амплитуды колебаний.

58. ТЕРМОДИНАМИКА раздел прикладной физики или теоретической теплотехники, в котором исследуется превращение движения в теплоту и наоборот. В термодинамике рассматриваются не только вопросы распространения теплоты, но и физические и химические изменения, связанные с поглощением теплоты веществом, а также, наоборот, выделение теплоты в ходе физических и химических превращений.

Первое начало термодинамики – это количественное выражение закона сохранения и превращения энергии.

Закон сохранения и превращения энергии является универсальным законом природы и применим ко всем явлениям. Он гласит: «запас энергии изолированной системы остается неизменным при любых происходящих в системе процессах; энергия не уничтожается и не создается, а только переходит из одного вида в другой».

59. Второй закон связан с понятием энтропии, являющейся мерой хаоса (или мерой порядка). Второй закон термодинамики гласит, что для вселенной в целом энтропия возрастает.

Существует два классических определения второго закона термодинамики:

· Кельвина и Планка

Не существует циклического процесса, который извлекает количество теплоты из резервуара при определенной температуре и полностью превращает эту теплоту в работу. (Невозможно построить периодически действующую машину, которая не производит ничего другого, кроме поднятия груза и охлаждения резервуара теплоты)

· Клаузиуса

Не существует процесса, единственным результатом которого является передача количества теплоты от менее нагретого тела к более нагретому. (Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара)

Оба определения второго закона термодинамики опираются на первый закон термодинамики, утверждающий, что энергия убывает.

Второй закон связан с понятием энтропии (S).

Энтропия порождается всеми процессами, она связана с потерей системы способности совершать работу. Рост энтропии - стихийный процесс. Если объем и энергия системы постоянны, то любое измение в системе увеличивает энтропию. Если же объем или энергия системы меняются, энтропия системы уменьшается. Однако, энтропия вселенной при этом не уменьшается.

Для того, чтобы энергию можно было использовать, в системе должны быть области с высоким и низким уровнями энергии. Полезная работа производится в результате передачи энергии от области с высоким уровнем энергии к области с низким уровнем энергии.

Дата добавления: 2015-04-24