Билет 3

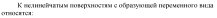
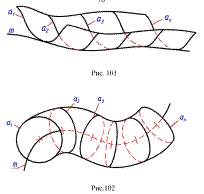
2. Если плоскость вращать вокруг ее следа до совмещения с плоскостью проекций, в котором расположен этот след, то геометрические образы, расположенные в плоскости, изобразятся без искажения. Этот способ является частным случаем вращения вокруг горизонтали или фронтали, так как горизонтальный след плоскости можно рассматривать как, а фронтальный след - как фронталь плоскости.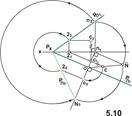

Билет 4.

1. Позиционные задачи – задачи, в которых требуется установить взаимное пересечение и взаимную принадлежность геометрических фигур. Решение задачи сводится к решению двух: построение точки, принадлежащей линии; построение точки, принадлежащей поверхности.

Пересечение двух плоскостей:

1. Вводим вспомогательную плоскость гамма

2. Построить линию пересечения а плоскостей альфа и гамма

3. Построим в пересечение плоскостей бета и гамма

4. Построить точку пересечения прямых а и в

5. Повторить n раз.

2.

Билет5.
1. Решение многих метрических задач требует применения перпендикулярных прямых и плоскостей и основывается на свойства прямоугольного проецирования прямого угла.

Прямой угол проецируется без искажения если обе стороны параллельны плоскости проекций. Если стороны угла не параллельны плоскости проекции, то угол проецируется с искажением на а эту плоскость проекции.

Теорему о проецировании прямого угла мы рассматривали при изучении свойств ортогонального проецирования. Напомним эту теорему.

Если хотя бы одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна, то угол на эту плоскость проецируется в натуральную величину.

Следствие: если прямоугольная проекция угла, одна сторона которого параллельна плоскости проекций, - прямой угол, то проецируемый угол также прямой.

Свойства проекций прямого угла имеют важное значение при решении метрических задач на чертеже, таких, как построение взаимно перпендикулярных прямых и плоскостей определения расстояния между геометрическими фигурами и т.д.

2. Общим методом построения разверток криволинейных поверхностей является метод триангуляции, при котором поверхность аппроксимируется (заменяется) вписанной или описанной многогранной поверхностью, грани которой – треугольники, а затем строится развертка многогранной поверхности, которая будет приближенной или условной разверткой криволинейной поверхности.
Этот метод применяется при построении развертки конической поверхности, которая аппроксимируется вписанной (реже описанной) пирамидальной поверхностью. Построение развертки конуса сводится к построению развертки пирамиды, у которой боковые грани являются треугольниками.
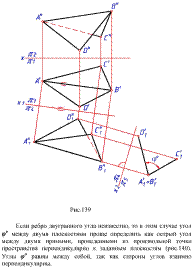
Рассмотрим построение пирамиды SABC (рис. 2).

Для построения развертки пирамиды необходимо знать длину каждого ребра. Основание пирамиды лежит в плоскости, параллельной плоскости П₁, а потому на эту плоскость отрезки АВ, АС и СB проецируются в истинную величину, и их длину можно измерить на горизонтальном поле проекций. Длины ребер AS, BS, CS находим вращением их вокруг горизонтальной оси i до фронтального положения, а потому S₁A₁, S₁B₁, S₁C₁ параллельны оси Х, фронтальные проекции S₂A₂, S₂B₂, S₂C₂ имеют длину, равную длине ребер пирамиды.
После того как найдены длины всех ребер, приступаем к построению развертки. Для этого на свободном чертеже построим треугольник А₀В₀S₀, равный грани АВS, причем |А₀S₀| = |A₂B₂|, |S₀B₀| = |S₂B₂|, где |A₀B₀| = |S₂C₂|, |A₀C₀| = |A₁C₁|, |B₀C₀| = |B₁C₁|. К боковой развертке примыкает основание А₀В₀С₀.
При построении развертки поверхности иногда приходится наносить линию, расположенную на ней, например линию пересечения с другой поверхностью. На рис. 2 показано построение линии а (1 2 3) (1₁ 2₁ 3₁, 1₂ 2₂ 3₂).

http://traffic.spb.ru/geom/part11/part11-2.html

Дата добавления: 2015-04-24