Билет 6

2.

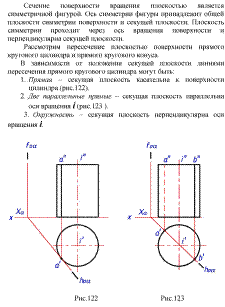
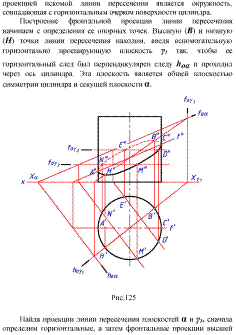
Билет 7.

2.

Билет 8.

1.

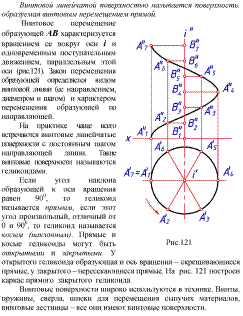
2.

Билет 9.

1.

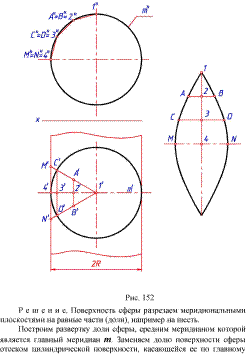
2.

Это расстояние равно длине общего перпендикуляра MN к заданным прямым АВ и CD (рис. 10.6). Для определения его длины удобно, чтобы одна из прямых располагалась перпендикулярно плоскости проекций. Для этого надо последовательно ввести две новые плоскости проекций.

П ₄ ½½ AB; П ₄ ^ П ₁; П ₄ Ç П ₁ = x ₁; x ₁ ½½ A ₁ B ₁;

П ₅ ^ AB; П ₅ ^ П ₄; П ₅ Ç П ₄ = x ₂; x ₂ ^ A ₄ B ₄.

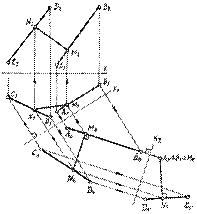Рис. 10.6.

На плоскость П ₅ прямая АВ проецируется в точку A ₅ º B ₅. Проведя перпендикуляр из точки A ₅ º B ₅ на проекцию C ₅ D ₅, находим проекцию N ₅ точки N пересечения его с прямой CD. Отметим проекцию M ₅ точки М, совпадающую с проекциями точек A ₅, B ₅. Искомое расстояние определено - M ₅ N ₅. На чертеже стрелками указано построение проекций M ₁ N ₁ и M ₂ N ₂ общего перпендикуляра к двум скрещивающимся прямым в системе П ₂ ^ П ₁.

Билет 10.

1. В пространстве прямая может либо принадлежать плоскости, либо не принадлежать плоскости. Это утверждение справедливо и для точки. Прямая принадлежит плоскости, если она проходит:

• Через две точки, принадлежащие плоскости;
• Через точку плоскости параллельно любой прямой этой плоскости.

Точка принадлежит плоскости, если она расположена на прямой (кривой), лежащей в данной плоскости.

Горизонталь – прямая, параллельная горизонтальной плоскости проекций. Фронталь – прямая, параллельная фронтальной плоскости проекций. Линиями наибольшего наклона плоскости к плоскостям проекций П1, П2 и П3 называются линии, лежащие в ней и перпендикулярные или к горизонталям, или к фронталям, или к профильным прямым. Линии наибольшего наклона позволяют определить углы наклона заданной плоскости к плоскостям проекций.

Точки, у которых проекции на П1 совпадают, называют конкурирующими по отношению к плоскости П1, а точки, у которых проекции на П2 совпадают, называют конкурирующими по отношению к плоскости П2.

Точки К и L конкурирующие по отношению к плоскости П1, так как на плоскости П1 точки К и L проецируются в одну точку: К1 = L1. Точка К выше точки L, т.к. К2 выше точки L2, потому К1 на П1 видима.

Точки N и М конкурирующие по отношению к плоскости П2, так как на плоскости П2 точки M и N проецируются в одну точку: М2 = N2.
Точка N ближе к наблюдателю, чем точка М, т.к. координата у точки N больше, чем у точки М, а потому точка N закрывает точку М, а потому N1 на П2 является видимой.

2. Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Алгоритм:

1. Плоскость  (рис. 4-19) задаём пересекающимися прямыми m  n = К. Согласно

вышесказанному, одна из них должна быть перпендикулярна плоскости Г. Пусть это будет n.

2. В плоскости Г берём горизонталь и фронталь.

3. Через точку К1 проводим n1  h1, а через К2 проводим n2  f2, следовательно, n  Г.

4. Прямую m, проходящую через точку К, задаём произвольно.

Таким образом, (n  m)  Г(АВС).

Билет 12.

1.

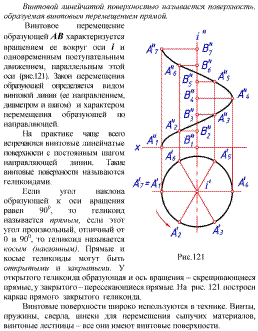
2.

1. Если хотя бы одна из сторон прямого угла параллельна плоскости проекций, а другая не перпендикулярна ей, то на эту плоскость прямой угол проецируется без искажения

2. Если проекция угла представляет угол 900, то проецируемый угол будет прямым лишь при условии, что одна из сторон этого угла параллельна плоскости проекций

3. Если обе стороны любого угла параллельны плоскости проекций, то его проекция равна по величине проецируемому углу.

4. Если стороны угла параллельны плоскости проекций или одинаково наклонены к ней, то деление проекции угла на этой плоскости пополам соответствует делению пополам и самого угла в пространстве.

5. Если стороны угла не параллельны плоскости проекций, то угол на эту плоскость проецируется с искажением.

Билет 13.

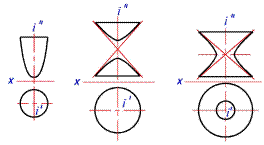Параболоид вращения Двуполостный и однопол гиперболоид

2.

Билет 14.

2.

Билет 15.

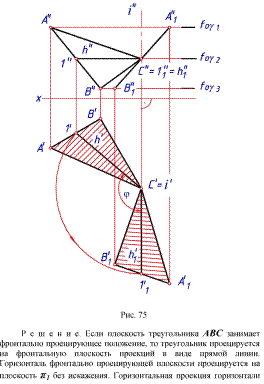
2.

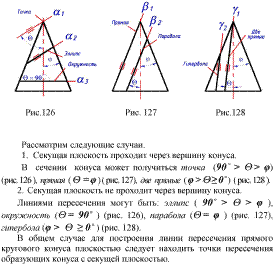
Рассмотрим частный случай, когда основание призмы на одну из плоскостей проекций проецируется в натуральную величину (рис. 140).

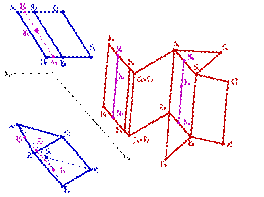
Развертка боковой поверхности такой призмы осуществляется способом раскатки. Этот способ заключается в следующем. Сначала, как и в предыдущем примере, преобразуют эпюр так, чтобы боковые ребра призмы стали параллельны одной из плоскостей проекций.

Затем новую проекцию призмы вращают вокруг ребра С₄F₄ до тех пор пока грань ACDF не станет параллельной плоскости П₄. При этом положение ребра С₄F₄ остается неизменным, а точки принадлежащие ребру AD перемещаются по окружностям, радиус которых определяется натуральной величиной отрезков AC и DF (так как основания призмы параллельны П₁, то на эту плоскость проекций они проецируются без искажения, т.е. R=A₁C₁=D₁F₁), расположенных в плоскостях, перпендикулярных ребру С₄F₄. Таким образом, траектории движения точек A и D на плоскость П₄ проецируются в прямые, перпендикулярные ребру С₄F₄.

Когда грань ACDF станет параллельна плоскости П₄, она проецируется на неё без искажения, т.е. вершины A и D окажутся удаленными от неподвижных вершин C и F на расстояние, равное натуральной величине отрезков AC и DF. Таким образом, засекая перпендикуляры, по которым перемещаются точки A₄ и D₄ дугой радиуса R=A₁C₁=D₁F₁, можно получить искомое положение точек развертки A₀ и D₀.

Следующую грань АBDE вращают вокруг ребра AD. На перпендикулярах, по которым перемещаются точки B₄ и E₄ делают засечки из точек A₀ и D₀ дугой радиуса R=A₁B₁=D₁E₁. Аналогично строится развертка последней боковой грани призмы.

Процесс последовательного нахождения граней призмы вращением вокруг ребер можно представить как раскатку призмы на плоскость параллельную П₄ и проходящую через ребро СF.

Построение на развертке точки К, принадлежащей боковой грани АBDE, ясно из рисунка. Предварительно через эту точку по грани провели прямую NМ, параллельную боковым ребрам, которая затем построена на развертке.

Билет 16.

1.

2.

Билет 19.

1.

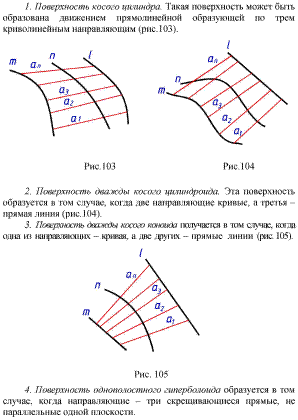
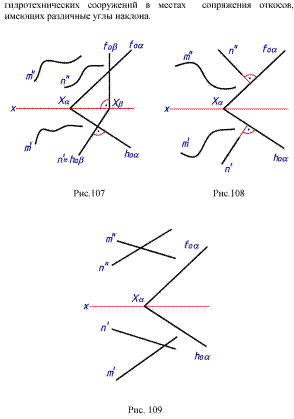
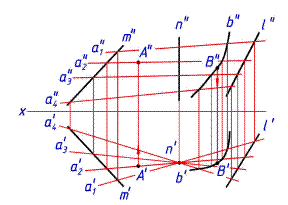
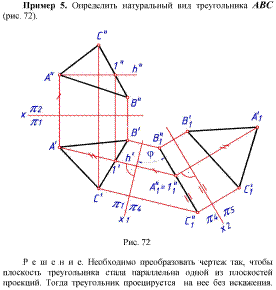
2. Аналогичные выводы можно сделать и для вращения вокруг фронтально проецирующей прямой. При вращении плоской фигуры вокруг оси, перпендикулярной плоскости проекций, проекция ее на эту плоскость не изменяется ни по величине, ни по форме, так как не изменяется наклон плоской фигуры к этой плоскости, а меняется лишь положение этой проекции относительно линии связи. Вторая же проекция на плоскости, параллельной оси вращения, изменяется и по форме, и по величине. Проекции точек на этой плоскости проекций находятся на прямых, перпендикулярных исходным линиям связи. Пользуясь этими свойствами, можно применить для преобразования чертежа способ вращения, не задаваясь изображением оси вращения и не устанавливая величину радиуса вращения. Это — способ плоскопараллельного перемещения, при котором все точки геометрической фигуры перемещаются во взаимно параллельных плоскостях без изменения действительного вида и размеров этой фигуры (рис. 117).

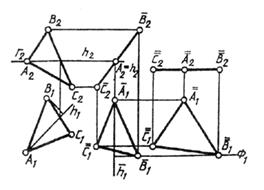
Треугольник ABC занимает общее положение. Первым плоскопараллельным перемещением он поставлен во фронтально проецирующее положение с помощью горизонтали h, которую расположим как фронтально проецирующую прямую в ее плоскости вращения Г || П. При этом А1В1С1 = А1В1С1, а плоскости вращения точек В и С параллельны плоскости Г.

Вторым перемещением АВС расположен параллельно плоскости П1. Без изменения оставлена вырожденная фронтальная проекция треугольника (А2В2C2 = А2В2С2), а новая горизонтальная проекция, дающая истинную величину АВС, получена построением новых горизонтальных проекций точек А1В1 и С1 в результате их вращения в параллельных фронтальный плоскостях уровня (B2 ~ Ф; B ~ Ф).

Билет 20.

Пространственные кривые линии в начертательной геометрии обычно рассматриваются как результат пересечения поверхностей или траекторию движения точки.

Пространственную, так же как и плоскую, кривую линию на чертеже задают последовательным рядом точек.

Классическим примером пространственных кривых линий являются цилиндрическая и коническая винтовые линии.

Кривые линии, все точки которых принадлежат одной плоскости, называются плоскими

Коническая поверхность образуется движением прямой линии, скользящей по некоторой неподвижной замкнутой или незамкнутой кривой и проходящей во всех своих положениях через неподвижную точку

Конические поверхности, имеющие ось, в зависимости от вида нормального сечения бывают:
1) круговые - нормальное сечение круг
2) эллиптические - нормальное сечение эллипс

Билет 21.

Расстояние от точки до прямой определяется длиной перпендикуляра, опущенного из точки на прямую.

Проведем через точку М плоскость S, перпендикулярную прямой 1 (рис.10.4). Зададим эту плоскость двумя пересекающимися прямыми - горизонталью и фронталью. В этом случае горизонтальная проекция горизонтали будет перпендикулярна горизонтальной проекции прямой 1. Фронтальная проекция фронтали - перпендикулярна фронтальной проекции прямой 1.

Построим точку встречи прямой 1 с плоскостью S, l Ç S = К. Так как прямая 1 перпендикулярна плоскости S, следовательно, она перпендикулярна любой прямой, принадлежащей плоскости S, в том числе - и прямой МК, т.е. прямая МК перпендикулярна прямой 1.

Отрезок МК спроецировался с искажением. Его натуральную величину найдем способом вращения вокруг фронтально проецирующей прямой, проходящей через точку М. ½ M ₁ K ₁ ½ = ½ MK ½.

Решение задачи методом проецирования на дополнительную плоскость приведено на рис.10.5 в следующем разделе. ½ M ₅ K ₅ ½ = ½ MK ½.

Билет 22.

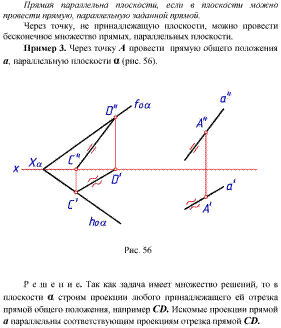
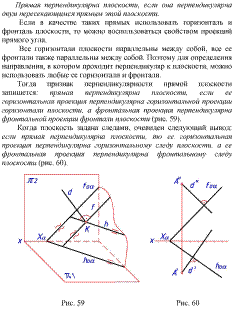
1) Если прямая, лежащая вне плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельна этой плоскости.

2) Если прямая и плоскость перпендикулярны одной и той же прямой, то они параллельны.

Билет 23.

2.

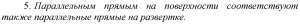
1. призма рассекается перпендикулярной к ее ребрам или граням плоскостью. Фронтально проецирующая плоскость Р₂ горизонтально след которой на эпюре не показан;

2. строится проекция и определяется истинная величина фигуры нормального сечения. На риуснке 6.12 фронтальная проекция фигуры сечения (1-2-3) совпадает со следом секущей плоскости, а горизонтальная не показана. Истинная величина фигуры сечения (1₀-2₀-3₀) построена способом совмещения - плоскость Р вращением вокруг ее горизонтального следа совмещена с плоскостью проекции П₁;

3. истинная величина фигуры нормального сечения на свободном поле чертежа разворачиваеться в прямую линию (1₀-1₀) и от точек 1₀, 2₀, 3₀, 1₀ проводятся перпендикуляры к прямой 1₀-1₀;

4. На перпендикулярах по обе стороны от точек 1₀, 2₀, 3₀, 1₀ откладываются истинные величины соответствующих ребер призмы и полученные точки a₁, b₁, c₁, a₁ и a′₁, b′₁, c′₁, a′₁ соединяются отрезками прямых. В рассматриваемом примере ребра призмы параллельны плоскости проекции П₂, а следовательно истинными величинами их являются соответствующие фронтальные проекции.

Билет 24.

Кривая – это множество точек пространства, координаты которых являются функциями одной переменной. Термин «кривая» в разных разделах математики определяется по разному. В начертательной геометрии кривую рассматривают как:

• траекторию, описанную движущейся точкой,
• проекцию другой кривой,
• линию пересечения двух поверхностей.

Кривые подразделяются на алгебраические и трансцендентные в зависимости от того являются ли их уравнение алгебраическими или транцендентными в прямоугольной системе координат. Множество алгебраических кривых в свою очередь подразделяются на множество в зависимости от порядка кривой, определяемого степенью ее уравнения.

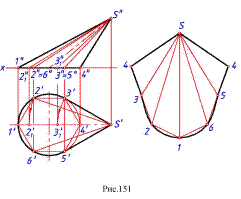
Для построения линии пересечения линейчатой поверхности плоскостью в общем случае строят точки пересечения прямолинейных образующих поверхности с секущей плоскостью, т.е. находят точки пересечения прямой с плоскостью. Искомую кривую проводят через эти точки.

Для построения линии пересечения линейчатой поверхности с плоскостью в общем случае применяют вспомогательные секущие плоскости. Точки искомой линии определяются в пересечении линий, по которым вспомогательные секущие плоскости пересекают данные поверхность и плоскость.

Дата добавления: 2015-04-24