Вероятностные запросы

Байесовская сеть позволяет получить ответы на следующие типы вероятностных запросов^[2]:

§ нахождение вероятности свидетельства,

§ определение априорных маргинальных вероятностей,

§ определение апостериорных маргинальных вероятностей, включая:

прогнозирование, или прямой вывод, — определение вероятности события при наблюдаемых причинах,

диагностирование, или обратный вывод (абдукция), — определение вероятности причины при наблюдаемых следствиях,

межпричинный (смешанный) вывод (intercausal inference) или трансдукция, — определение вероятности одной из причин наступившего события при условии наступления одной или нескольких других причин этого события.

§ вычисление наиболее вероятного объяснения наблюдаемого события (Most probable explanation, MPE),

§ вычисление апостериорного максимума (Maximum a-posteriori, MAP).

Байесовские сети используются для моделирования в биоинформатике (генетические сети, структура белков), медицине, классификации документов, обработке изображений, обработке данных и системах поддержки принятия решений.

Теорема Байеса, Формула Байеса — одна из основных теорем элементарной теории вероятностей, которая определяет вероятность того, что произошло какое-либо событие (гипотеза), имея на руках лишь косвенные тому подтверждения (данные), которые могут быть неточны. Названа в честь ее автора, преп. Реверенда Томаса Байеса (посвященная ей работа «An Essay towards solving a Problem in the Doctrine of Chances» впервые опубликована в 1763 году, через 2 года после смерти автора). Полученную по формуле вероятность можно далее уточнять, принимая во внимание данные новых наблюдений.Психологические эксперименты показали, что люди при оценках вероятности игнорируют различие априорных вероятностей (ошибка базовой оценки), и потому правильные результаты, получаемые по теореме Байеса, могут очень отличаться от ожидаемых. Формула Байеса: 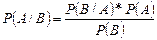гдеP(A) — априорная вероятность гипотезы A (смысл такой терминологии см.;P(A | B) — вероятность гипотезы A при наступлении события B (апостериорная вероятность);P(B | A) — вероятность наступления события B при истинности гипотезы A;

P(B) — вероятность наступления события B.

Условная вероятность — вероятность одного события при условии, что другое событие уже произошло.

Условной вероятностью события A при условии, что произошло событие B, называется число: 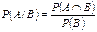Условная вероятность определена только в случае, когда

Дата добавления: 2015-04-24