Строение электронных оболочек атома. Волновая теория строения атома. Понятие об электронном облаке

Химические газовые законы. Закон Авогадро. Молярный объем.

Закон Авогадро: в равных объемах различных газов при одинаковых условиях (температура и давление) содержится одинаковое число молекул.

Следствие 1: один моль любого газа при одинаковых условиях занимает один и тот же объем. Молярный объем любого газа при н.у. равен 22,4 л/моль

Следствие 2: молярная масса (а значит и относительная атомная масса) вещества в газообразном состоянии равна его удвоенной плотности по водороду.

Если в равных объемах газов при одинаковых условиях содержится одинаковое число молекул, то очевидно, то отношение масс равных объемов газов будет равно отношению их молекулярных масс или отношению численно равных им молярных масс: m₁/m₂=M₁/M_2.

Отношение массы объема одного газа к массе такого же объема другого газа (взятого при тех же условиях) называется плотностью первого газа по второму: M₁/M₂=D и M₁=M₂D

При нормальных условиях 1 моль любого газа, занимает объем, равный 22,4 л – этот объем называется молярным объемом газа: V_m=22,4 л. Очевидно, молярный объем есть отношение объема вещества (V) к количеству этого вещества (n): V_m= V/ n.

Закон Авогадро дал объяснение правилу Гей-Люсака: объемы газов, участвующих в реакции, относятся между собой как их стехиометрические коэффициенты – закон объемных отношений – используют для количественных расчетов реагентов, находящихся в газовом состоянии.

Зависимость объема газа от его давления при постоянной температуре (т.е. в изотермических условиях) была показана в законе Бойля-Мариота: pV=cоnst и V=conct/p.

Закон Шарля-Гей-Люсака вскрывает зависимость объема газа от его температуры при постоянном давлении (т.е. в изобарных условиях): V=V₀T/T₀, где T - абсолютная температура газа, V₀- объем газа при T₀ =273,15К или 0 ⁰С.

На основании законов Бойля-Мариота, Шарля-Гей-Люсака и с учетом закона Авогадро выводится объединенный закон газового состояния, выражением которого является уравнение состояния идеального газа (идеальный газ – газ, частицы которого практически не взаимодействуют друг с другом): pV/T=p₀V₀/T₀. При замене V₀ на V_m, при тех же условиях, в формулу вводится n: pV/T=np₀Vm₀/T₀.

p₀Vm₀/T₀=R=62360 мм РТ ст*мл/(моль*К)=8,314 Дж/(моль*К) – универсальная газовая постоянная – используя её мы получаем уравнение Клайперон-Менделеева: pV=(m/M)*RT

Атом состоит из ядра и электронной оболочки.

Атомное ядро - центральная часть атома, состоящая из Z протонов и N нейтронов, в которой сосредоточена основная масса атомов.

Электронная оболочка – это совокупность всех электронов в данном атоме.

Первоначально были предложены две модели атома.

1. Согласно модели Томсона, атом состоит из положительного заряда, равномерно распределенного по всему объему атома, и электронов, колеблющихся внутри этого заряда.

2. Резерфордом была предложена планетарная модель атома. Согласно этой модели, атом состоит из положительно заряженного ядра, в котором сосредоточена преобладающая часть массы атома, и вращающихся вокруг него электронов. Эта модель первоначально не могла объяснить устойчивость атома, т.к. вращающийся вокруг ядра электрон должен излучать энергию. Вторым противоречием этой модели была невозможность объяснить линейчатый характер атомных спектров, т.е. излучение атомом электромагнитных волн только с определенными длинами волн.

Для устранения этих противоречий Бор дополнил планетарную модель атома на основе следующих предположений (постулаты Бора):

1) Электрон может вращаться вокруг ядра не по любым орбитам, а лишь по некоторым определенным (стационарным) орбитам, на которых он не излучает энергии.
2) Ближайшая к ядру орбита соответствует наиболее устойчивому состоянию атома. При сообщении энергии извне электрон может перейти на одну из более удаленных орбит (возбужденное состояние атома).
3) Поглощение и излучение энергии атомом может происходить только при переходе электрона с одной орбиты 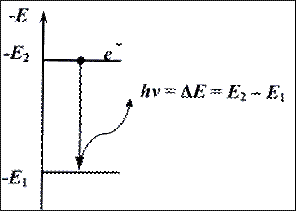на другую. При этом разность энергий начального и конечного состояний воспринимается или отдается в виде кванта лучистой энергии. Этому излучению соответствует частота колебаний ν, выражаемая уравнением Планка: hν = E_н – E_к, где h – постоянная Планка (h=6,62 ×10–34 Дж×с); Е_н, Е_к – соответственно энергии начального и конечного состояний.

Для того, чтобы объяснить, почему имеет место квантование энергетических уровней (существование стационарных орбит), в 1924 г. де Бройлем была выдвинута гипотеза, что каждая движущаяся частица одновременно обладает свойствами волны, длина которой λ = h/(m ^. v), где m – масса частицы, v – ее скорость. Эта гипотеза основывалась на последних достижениях физики того времени (например, было уже известно, что свет имеет двойственную природу, обладая свойствами электромагнитной волны с λ = с/ν и одновременно свойствами потока частиц – фотонов с энергией каждого Е = hν). Гипотеза де Бройля экспериментально подтверждается дифракцией электронов в кристаллах и позволяет объяснить существование стационарных орбит. Электрон может без потери энергии находиться на тех орбитах, в которых укладывается целое число волн де Бройля. В этом случае соблюдается условие существования стоячей волны.

Возможность рассматривать каждую частицу одновременно как волну называется корпускулярно-волновым дуализмом. Из него вытекает соотношение неопределенностей Гейзенберга. Согласно классической механике, движение материальной точки однозначно описывается значениями координат и импульса. Импульсом называется произведение массы объекта на его скорость: p = mv. В случае микрообъектов, когда движение происходит в соответствии с законами квантовой механики, описать координаты и скорость с любой точностью принципиально невозможно.

Волновое уравнение - Согласно квантовой механике, движение электрона в атоме описывается волновым уравнением (уравнение Шредингера):
+ U ^. Y = E ^. Y, где Y – волновая функция; m – масса электрона. Масса покоя электрона m_e = 9,109.10^-31 кг; U – потенциальная энергия; E – полная энергия электрона; x, y, z – координаты электрона в системе с центром в ядре атома.

Решением уравнения Шредингера является волновая функция Y и соответствующее ей значение энергии электрона E. Вероятность нахождения электрона в пространстве характеризуется квадратом волновой функции. Квадрат волновой функции в данной точке пространства |Y|² – это плотность вероятности обнаружения электрона в этой точке пространства. Значит величина |Y|^2. dv – вероятность обнаружить электрон в области пространства dv. Вероятность обнаружить электрон в какой-нибудь точке пространства равна единице, т.е. 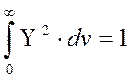, причем величина волновой функции вдали от ядра атома близка к нулю и, поэтому электрон находится вблизи ядра. Электронное облако – область пространства, ограниченная поверхностью одинакового значения величины волновой функции электрона, вероятность обнаружения электрона в которой составляет 0,9 (или 90%).

Таким образом, в квантовомеханической (вероятностной) модели атома исчезает смысл орбиты, на которой находится электрон. Взамен ее мы имеем дело с электронной плотностью, “размазанной” в пространстве атома. Наличие трех измерений пространства приводит к тому, что в выражении волновой функции Y, являющейся решением уравнения Шредингера, появляются три величины, которые могут принимать только дискретные целочисленные значения – три квантовых числа. Они обозначаются символами n, ℓ и m_l. Эти квантовые числа характеризуют состояние электрона не только в атоме водорода, но и в любом другом атоме.

3.

Дата добавления: 2015-04-24