Изменение свободной энергии равно максимальной полезной работе, которую совершает система в изобарно-изотермическом процессе

Энергия Гиббса. Соотношение между энергией Гиббса, энтальпией и энтропией. Стандартная энергия Гиббса образования вещества. Изменение энергии Гиббса в ходе реакции и направление самопроизвольного протекания реакции.

Факторы, определяющие направление самопроизвольного протекания химических процессов (энергетический и энтропийный). Энтропия. Второе и третье начала термодинамики. Определение изменения энтропии в ходе реакции.

Второй закон (начало) термодинамики: Ограниченность первого начала термодинамики заключается в том, что оно не определяет направления обмена тепловой энергией между телами. Первое начало не запрещает переход тепла от менее нагретого тела к более нагретому. Суть второго начала состоит в том, что оно определяет направление самопроизвольного протекания процессов, в том числе и химических реакций.

Самопроизвольным называется процесс, который протекает самостоятельно без воздействия внешних факторов. Например, если соединить два сосуда — заполненный газом и пустой, то газ самопроизвольно заполнит весь объем. Взаимодействие металлического натрия с водой при н. у. также происходит самопроизвольно. Обратные процессы можно осуществить, оказав внешнее воздействие. Для исследователя необходимо иметь критерий, с помощью которого можно было бы предсказать направление самопроизвольного протекания процесса.

Существует еще одна функция состояния, которая с учетом первого начала термодинамики позволяет предсказать направление протекания процесса в изолированных системах. Такой функцией состояния является энтропия (S). Интерпретировать энтропию можно как с точки зрения макроскопического состояния системы, так и с точки зрения микроскопического.

Третье начало термодинамики: Еще один важный принцип химической термодинамики был установлен в первой четверти 20 в. В. Нернстом. Он экспериментально установил, что, когда температура приближается к абсолютному нулю, стандартные энтропии DS° для многих химических реакций стремятся к нулю. Поскольку этот результат не следует из первого и второго начал термодинамики, он получил название третьего начала термодинамики. Оно не имеет столь же общего характера, как первые два начала, однако большинство очевидных исключений или аномалий получило удовлетворительное объяснение с учетом особенностей кристаллического строения конкретных веществ.
Значение принципа Нернста состоит в том, что зависимость энтропии реакции от температуры может быть выведена, согласно термодинамической теории, исключительно из данных по теплоемкости для отдельных участвующих в реакции веществ. Это значит, что, если известно значение DS° при какой-либо одной температуре (при T = 0 DS° = 0), значения энтропии реакции при других температурах вычисляются исключительно из тепловых измерений. Аналогично этому, величина DH° может быть получена из калориметрических данных путем непосредственного измерения теплоты данной реакции либо косвенно, путем измерения теплот других реакций и применения закона Гесса. Следовательно, подстановка полученных значений DH° и DS° в уравнение (9) или (11) дает гиббсову энергию или константу химического равновесия исключительно из тепловых измерений. Это позволяет предвидеть направление и равновесное состояние химической реакции еще до того, как найден способ ее проведения.
Для практического применения третьего начала термодинамики требуются точные результаты измерений теплоемкости вплоть до самых низких доступных температур, желательно до температуры жидкого гелия (около 4 К). Это направление термодинамических исследований химических явлений стимулировали криогенные исследования, выполненные в последние десятилетия.

Определение энтропии с позиций классической термодинамики: Если рассматривать систему в целом, то в обратимом процессе, протекающем при постоянной температуре, изменение энтропии будет равно: D S = [19]

Для необратимого процесса это равенство превращается в неравенство:D S > [20]

Поскольку энтропия является функцией состояния, то ее изменение не зависит от пути перехода системы из одного состояния в другое, а определяется только значениями энтропии для системы в исходном и конечном состояниях. Размерность энтропии [S]=Дж/моль·К.

Существует много формулировок второго начала термодинамики. Приведем одну из них.

В изолированной системе самопроизвольно протекают только те процессы, которые сопровождаются увеличением энтропии.

В самопроизвольном процессе DS>0;

в равновесном процессе DS=0;

в не самопроизвольном процессе DS< 0.

В случае изотермического процесса для идеального газа изменение внутренней энергии равно нулю, отсюда, согласно уравнению [3]: Q_обр.= -А _{расш р}. [ 21 ]

[22]

Используя уравнение Менделеева-Клапейрона, получим: [23]

Скомбинировав выражения [19], [21] и [23], получим для изменения энтропии в изотермическом процессе расширения одного моля идеального газа:DS=Rln [24]

Из определения С_р и уравнений [19] и [18] можно получить зависимость изменения энтропии от температуры: [25]

или в частном случае, если АС_Р не зависит от температуры: D S = D АС_р-lп [26]

Статистическая интерпретация понятия энтропии

Больцман вывел соотношение, связывающее абсолютную энтропию с числом микроскопических состояний системы, соответствующих данному макроскопическому состоянию (или термодинамической вероятностью): S = kּ1пW, [27]

Где k =R/N_A = 1,38 • 10 ²³Дж • К ^-1 — постоянная Больцмана, а W— число микроскопических состояний системы.

Макроскопическое состояние включает в себя множество микроскопических состояний. Их число для различных систем может подсчитываться по-разному. По Больцману макроскопическое состояние определяется количеством частиц на каждом энергетическом уровне. Частицы имеют свой номер, а полная энергия системы постоянна. Микроскопические состояния отличаются друг от друга распределением частиц по уровням энергий.

В термодинамике мы имеем дело с системами, состоящими из огромного числа частиц, с множеством макросостояний с различными W.

Из формулировки второго начала термодинамики следует, что в изолированной системе при самопроизвольном процессе энтропия возрастает. Система будет самопроизвольно стремиться к макросостоянию с максимальным W. Отсюда энтропию можно рассматривать как меру хаоса системы.

При абсолютной температуре Т = 0К чистые химические вещества образуют идеальные кристаллы, и их состояние можно описать только одним способом (W = 1), а логарифм единицы равен нулю. Согласно выражению [27], и энтропия при этой температуре равна нулю. Пользуясь этим, можно сформулировать третье начало термодинамики как: Энтропия химических веществ при абсолютном нуле равна нулю.

Таким образом, энтропия является единственной функцией состояния, для которой можно рассчитать абсолютное значение:

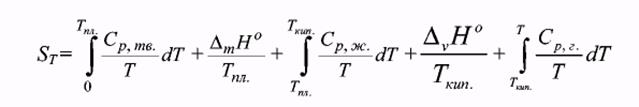
Второй закон термодинамики дает критерии для самопроизвольности протекания процессов (DS>0) и равновесия (DS = 0) в изолированных системах, которые практически не существуют. Можно применить второй закон термодинамики к неизолированным системам, поддерживаемым при постоянной температуре. Кроме того, предполагается, что система сохраняет постоянный объем или постоянное давление.

Направление протекания реакций: Рассмотрим возможность самопроизвольного протекания химической реакции в зависимости от знака энтальпийного и энтропийного членов в выражении изменения свободной энергии. Если изменение свободной энергии меньше нуля, то реакция протекает самопроизвольно. Если ∆G = 0, начальные и конечные состояния могут существовать в равновесии. Если же изменение свободной энергии больше нуля, самопроизвольное протекание реакции невозможно. Самопроизвольно протекает обратная реакция. А так как, согласно уравнению [32], изменение свободной энергии выражается через изменения энтальпии и энтропии (в предположении, что они не зависят от температуры), то их знаки будут определять знак ∆G. В ниже рассмотренных примерах принимается, что парциальные давления всех газообразных участников реакций равны по одной атмосфере, т.е. ∆G_г=∆G°_г. В этом случае можно использовать в расчётах стандартные изменения энтальпии и энтропии. Возможны четыре случая.

Первый: когда изменение энтальпии отрицательно, а изменение энтропии положительно, то изменение свободной энергии всегда отрицательно. Такие реакции самопроизвольно протекают в прямом направлении. Примером может служить реакция горения черного пороха, которая протекает по следующему суммарному уравнению:

2 КNO₃ + 3С + S =N₂ + ЗСО₂ + К₂S

Для этой реакции:

D_Г H⁰₂₉₈ = D _f H⁰₂₉₈ N₂ + 3D _f H⁰₂₉₈ CO₂ + D _f H⁰₂₉₈ K₂S - 2D _f H⁰₂₉₈ KNO₃ - 3D _f H⁰₂₉₈ C - D _f H⁰₂₉₈ S = - 582,41 кДж,

D_r S = S⁰₂₉₈N₂ + 3 S⁰₂₉₈ CO₂ + S⁰₂₉₈ K₂S - 2 S⁰₂₉₈ KNO₃ - 3 S⁰₂₉₈ C - S⁰₂₉₈ S = 630,34Дж/К

Следовательно,

D_rG⁰₂₉₈ = - 582,41-298ּ630,34ּ10^-3 = -770,25 кДж<0,

и реакция протекает самопроизвольно.

Второй: когда изменение энтальпии положительно, а изменение энтропии отрицательно. Эти реакции в прямом направлении самопроизвольно не идут, самопроизвольно протекает обратная реакция. В качестве примера приведем реакцию термического разложения хлористого водорода на простые вещества: 2 НС1_Г = Н₂,_г + С1₂,_г

Изменение энтальпии этой реакции равно двум энергиям разрыва связей Н—С1 и составляет 92,3 х 2 = 184,6 кДж. Изменение энтропии равно:D_rS⁰₂₉₈ = S⁰₂₉₈ H₂ + S⁰₂₉₈ Cl₂ - 2 S⁰₂₉₈ HCl = 130,6 + 233 - 2ּ186,7 = -19.8 Дж/К

D_rG⁰₂₉₈ = 184,6 - 298× (-19,8) ×10~³ = 190,5 кДж > О

Третий: когда как изменение энтальпии, так и энтропии отрицательны. В этом случае направление самопроизвольного процесса определяется температурой. При низкой температуре самопроизвольно идет прямая реакция, так как по абсолютной величине изменение энтальпии больше произведения температуры на изменение энтропии. Например, в реакции образования хлорида аммония из газообразных хлористого водорода и аммиака:

NН₃,г + НС1_Г =NH₄С1_К

D_гH⁰₂₉₈ = D _f H⁰₂₉₈ NH₄Cl - D _f H⁰₂₉₈ Cl₂ - D _f H⁰₂₉₈ NH₃ = -315,4-(-92,3)-(-46,2) = -176,9 кДж

D_r S = S⁰₂₉₈ NH₄Cl - S⁰₂₉₈ NH₃ - S⁰₂₉₈ HCl = 94,6 – 192,5 – 186,7 = -284,6 Дж/К

Т. к. при равновесии изменение свободной энергии равно нулю (DG = 0), то температура, при которой система находится в равновесии, равна 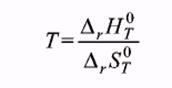[59]

И Т = 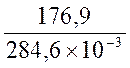= 621,6К

Четвертый: когда изменение энтальпии и энтропии положительные. Направление реакции также зависит от температуры: при низкой температуре самопроизвольно будет протекать обратная реакции, а при высокой — прямая.

Это характерно для реакций диссоциации: N₂O₄ «2 N0₂

Для данной реакции D _г H⁰₂₉₈= 57,З кДж; D _г S⁰₂₉₈ = 1 76,6 Дж/К и D_rG°₂₉₈ = 4,7 кДж.

Температура, при которой устанавливается состояние равновесия: Т= 324,5 К. Ниже этой температуры самопроизвольно протекает реакция димеризации, а выше — реакция диссоциации.

Следует отметить, что стандартные величины образования изобарно-изотермического потенциала простых веществ (так же как и стандартные энтальпии образования простых веществ) принимаются равными нулю. Например: Δ_fG⁰(H₂) = 0.

Свободная энергия Гиббса: Согласно второму началу термодинамики при постоянном давлении и температуре для обратимого процесса: Q_p - T D S = D H_T -T D S_T =0 [29]

а для необратимого процесса D Н_Т - Т D S_Т <0. [30]

Разность, описываемая уравнением [30], представляет собой новую функцию состояния, так как является разностью двух функций состояния: энтальпии и энтропии, умноженной на температуру, которая, в свою очередь, подпадает под определение функции состояния. Называется эта функция свободной энергией Гиббса (или изобарно-изотермическим потенциалом), обозначается буквой Gи имеет размерность кДж/моль.

Изменение свободной энергии в процессе равно:

D G = D Н-Т D S -S D T. [31]

При постоянной температуре, когда ΔТ=0, уравнение [31] превращается в следующее равенство: D G = D Н-Т D S. [32]

Согласно первому началу термодинамики, изменение внутренней энергии системы равно сумме теплоты, выделенной или поглощенной в результате химической реакции или другого процесса, и полной работы, совершенной системой [2]. Полная работа процесса, протекающего при постоянных давлении и температуре, складывается из работы против сил давления и полезной работы: А = - р D V+А_полезн [33]

Подставив в уравнение [32] значение изменения энтальпии [7], получим:D G = D U - Т D S+р D V [34]

Комбинируя уравнения [2], [19] и [33] с уравнением [34], для изменения свободной энергии Гиббса получим:

D G = - р D V + А_полезн + Т D S+р D V - Т D S.

Сократив подобные члены, получим выражение:

DG = A_полезн. [35]

Из выражения [35] вытекает физический смысл изменения свободной энергии Гиббса:

Иными словами, это энергия, которую можно «изъять» из системы в виде полезной работы. Поэтому она и называется «свободной».

Понятие свободной энергии Гиббса является результатом единства первого и второго законов термодинамики.

Направление протекания реакций: Рассмотрим возможность самопроизвольного протекания химической реакции в зависимости от знака энтальпийного и энтропийного членов в выражении изменения свободной энергии. Если изменение свободной энергии меньше нуля, то реакция протекает самопроизвольно. Если ∆G = 0, начальные и конечные состояния могут существовать в равновесии. Если же изменение свободной энергии больше нуля, самопроизвольное протекание реакции невозможно. Самопроизвольно протекает обратная реакция. А так как, согласно уравнению [32], изменение свободной энергии выражается через изменения энтальпии и энтропии (в предположении, что они не зависят от температуры), то их знаки будут определять знак ∆G. В ниже рассмотренных примерах принимается, что парциальные давления всех газообразных участников реакций равны по одной атмосфере, т.е. ∆G_г=∆G°_г. В этом случае можно использовать в расчётах стандартные изменения энтальпии и энтропии. Возможны четыре случая.

Первый: когда изменение энтальпии отрицательно, а изменение энтропии положительно, то изменение свободной энергии всегда отрицательно. Такие реакции самопроизвольно протекают в прямом направлении. Примером может служить реакция горения черного пороха, которая протекает по следующему суммарному уравнению:

2 КNO₃ + 3С + S =N₂ + ЗСО₂ + К₂S

Для этой реакции:

D_Г H⁰₂₉₈ = D _f H⁰₂₉₈ N₂ + 3D _f H⁰₂₉₈ CO₂ + D _f H⁰₂₉₈ K₂S - 2D _f H⁰₂₉₈ KNO₃ - 3D _f H⁰₂₉₈ C - D _f H⁰₂₉₈ S = - 582,41 кДж,

D_r S = S⁰₂₉₈N₂ + 3 S⁰₂₉₈ CO₂ + S⁰₂₉₈ K₂S - 2 S⁰₂₉₈ KNO₃ - 3 S⁰₂₉₈ C - S⁰₂₉₈ S = 630,34Дж/К

Следовательно,

D_rG⁰₂₉₈ = - 582,41-298ּ630,34ּ10^-3 = -770,25 кДж<0,

и реакция протекает самопроизвольно.

Второй: когда изменение энтальпии положительно, а изменение энтропии отрицательно. Эти реакции в прямом направлении самопроизвольно не идут, самопроизвольно протекает обратная реакция. В качестве примера приведем реакцию термического разложения хлористого водорода на простые вещества: 2 НС1_Г = Н₂,_г + С1₂,_г

Изменение энтальпии этой реакции равно двум энергиям разрыва связей Н—С1 и составляет 92,3 х 2 = 184,6 кДж. Изменение энтропии равно:D_rS⁰₂₉₈ = S⁰₂₉₈ H₂ + S⁰₂₉₈ Cl₂ - 2 S⁰₂₉₈ HCl = 130,6 + 233 - 2ּ186,7 = -19.8 Дж/К

D_rG⁰₂₉₈ = 184,6 - 298× (-19,8) ×10~³ = 190,5 кДж > О

Третий: когда как изменение энтальпии, так и энтропии отрицательны. В этом случае направление самопроизвольного процесса определяется температурой. При низкой температуре самопроизвольно идет прямая реакция, так как по абсолютной величине изменение энтальпии больше произведения температуры на изменение энтропии. Например, в реакции образования хлорида аммония из газообразных хлористого водорода и аммиака:

NН₃,г + НС1_Г =NH₄С1_К

D_гH⁰₂₉₈ = D _f H⁰₂₉₈ NH₄Cl - D _f H⁰₂₉₈ Cl₂ - D _f H⁰₂₉₈ NH₃ = -315,4-(-92,3)-(-46,2) = -176,9 кДж

D_r S = S⁰₂₉₈ NH₄Cl - S⁰₂₉₈ NH₃ - S⁰₂₉₈ HCl = 94,6 – 192,5 – 186,7 = -284,6 Дж/К

Т. к. при равновесии изменение свободной энергии равно нулю (DG = 0), то температура, при которой система находится в равновесии, равна 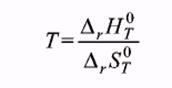[59]

И Т = 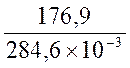= 621,6К

Четвертый: когда изменение энтальпии и энтропии положительные. Направление реакции также зависит от температуры: при низкой температуре самопроизвольно будет протекать обратная реакции, а при высокой — прямая.

Это характерно для реакций диссоциации: N₂O₄ «2 N0₂

Для данной реакции D _г H⁰₂₉₈= 57,З кДж; D _г S⁰₂₉₈ = 1 76,6 Дж/К и D_rG°₂₉₈ = 4,7 кДж.

Температура, при которой устанавливается состояние равновесия: Т= 324,5 К. Ниже этой температуры самопроизвольно протекает реакция димеризации, а выше — реакция диссоциации.

Следует отметить, что стандартные величины образования изобарно-изотермического потенциала простых веществ (так же как и стандартные энтальпии образования простых веществ) принимаются равными нулю. Например: Δ_fG⁰(H₂) = 0.

Дата добавления: 2015-04-24