
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Степенные средние
К степенным средним относятся такие наиболее известные и часто применяемые виды, как средняя геометрическая, средняя арифметическая и средняя квадратическая.
В качестве структурных средних рассматриваются мода и медиана.
Остановимся на степенных средних. Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными. Простая средняя считается по не сгруппированным данным и имеет следующий общий вид:
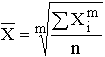 ,
,
где Xi – варианта (значение) осредняемого признака;
m – показатель степени средней;
n – число вариант.
Взвешенная средняя считается по сгруппированным данным и имеет общий вид
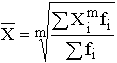 ,
,
где Xi – варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта;
m – показатель степени средней;
fi – частота, показывающая, сколько раз встречается i-e значение осредняемого признака.
Приведем в качестве примера расчет среднего возраста студентов в группе из 20 человек:
| № п/п | Возраст (лет) | № п/п | Возраст (лет) | № п/п | Возраст (лет) | № п/п | Возраст (лет) |
| 1 2 3 4 5 | 18 18 19 20 19 | 6 7 8 9 10 | 20 19 19 19 20 | 11 12 13 14 15 | 22 19 19 20 20 | 16 17 18 19 20 | 21 19 19 19 19 |
Средний возраст рассчитаем по формуле простой средней:
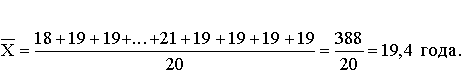
Сгруппируем исходные данные. Получим следующий ряд распределения:
| Возраст, Х лет | Всего | |||||
| Число студентов |
В результате группировки получаем новый показатель – частоту, указывающую число студентов в возрасте Х лет. Следовательно, средний возраст студентов группы будет рассчитываться по формуле взвешенной средней:
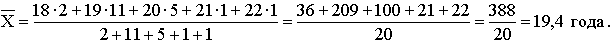
Общие формулы расчета степенных средних имеют показатель степени (m). В зависимости от того, какое значение он принимает, различают следующие виды степенных средних:
средняя гармоническая, если m = -1;
средняя геометрическая, если m –> 0;
средняя арифметическая, если m = 1;
средняя квадратическая, если m = 2;
средняя кубическая, если m = 3.
Формулы степенных средних приведены в табл. 4.4.
Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности средних: с увеличением показателя степени m увеличивается и соответствующая средняя величина:
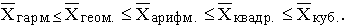
В статистической практике чаще, чем остальные виды средних взвешенных, используются средние арифметические и средние гармонические взвешенные.
Таблица 5.1
Виды степенных средних
| Вид степенной средней | Показатель степени (m) | Формула расчета | |
| Простая | Взвешенная | ||
| Гармоническая | -1 | 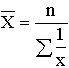
| 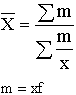
|
| Геометрическая | 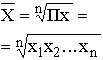
| 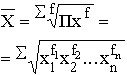
| |
| Арифметическая | 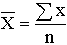
| 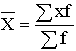
| |
| Квадратическая | 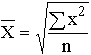
| 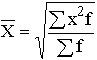
| |
| Кубическая | 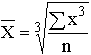
| 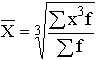
|
Средняя гармоническая имеет более сложную конструкцию, чем средняя арифметическая. Среднюю гармоническую применяют для расчетов тогда, когда в качестве весов используются не единицы совокупности – носители признака, а произведения этих единиц на значения признака (т.е. m = Xf). К средней гармонической простой следует прибегать в случаях определения, например, средних затрат труда, времени, материалов на единицу продукции, на одну деталь по двум (трем, четырем и т.д.) предприятиям, рабочим, занятым изготовлением одного и того же вида продукции, одной и той же детали, изделия.
Главное требование к формуле расчета среднего значения заключается в том, чтобы все этапы расчета имели реальное содержательное обоснование; полученное среднее значение должно заменить индивидуальные значения признака у каждого объекта без нарушения связи индивидуальных и сводных показателей. Иначе говоря, средняя величина должна исчисляться так, чтобы при замене каждого индивидуального значения осредняемого показателя его средней величиной оставался без изменения некоторый итоговый сводный показатель, связанный тем или другим образом с осредняемым [1]. Этот итоговый показатель называется определяющим, поскольку характер его взаимосвязи с индивидуальными значениями определяет конкретную формулу расчета средней величины. Покажем это правило на примере средней геометрической.
Формула средней геометрической
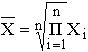
используется чаще всего при расчете среднего значения по индивидуальным относительным величинам динамики.
Средняя геометрическая применяется, если задана последовательность цепных относительных величин динамики, указывающих, например, на рост объема производства по сравнению с уровнем предыдущего года: i1, i2, i3,..., in. Очевидно, что объем производства в последнем году определяется начальным его уровнем (q0) и последующим наращиванием по годам:
qn=q0× i1× i2×...×in.
Приняв qn в качестве определяющего показателя и заменяя индивидуальные значения показателей динамики средними, приходим к соотношению
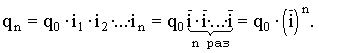
Отсюда
18. Структурные средние: мода и медиана
|
19. Статические ряды распределения: назначение, виды
Зарегистрированные в результате наблюдения индивидуальные значения изучаемого варьирующего признака образуют так называемый первичный ряд.
Первым шагом в упорядочении первичного ряда является его ранжирование. Располагая значения признака первичного ряда, например, в возрастающем порядке, получают ранжированный ряд.
Рассмотрим первичный ряд, полученный при регистрации уровня квалификации рабочих
Рассматривая этот ранжированный ряд, мы видим, что некоторые значения признака повторяются у разных рабочих (единиц совокупности).
Оформим результаты наблюдений более компактно, поставив в соответствие каждому значению признака подсчет численности единиц совокупности, имеющих одинаковые значения признаков.
Получим ранжированный (упорядоченный) ряд, характеризующий распределение изучаемого признака по единицам совокупности. В статистике такие ряды принято называть рядами распределения.
При достаточно большом числе единиц совокупности даже для несплошного наблюдения, приведенное выше упорядочение данных наблюдения может быть громоздким. Поэтому, такое ранжирование, как правило, сопровождается группировкой и сводкой. Изучаемый признак в этом случае является группировочным.
Отсюда общее определение:
Статистические ряды распределения – это упорядоченное расположение единиц изучаемой совокупности на группы по группировочному признаку.
Любой статистический ряд распределения состоит из двух элементов:
А) из упорядоченных значений признака или вариантов;
Б) количества единиц совокупности, имеющих данные значения, называемых частотами. Частоты, выраженные в долях единицы или в процентах к итогу, называются частостями.
Т.о., варианта – это отдельное значение (или вариант отдельной группы) варьируемого признака, которые он принимает в ряду распределения. Говоря о частотах надо иметь в виду, что сумма частот составляет объем изучаемой совокупности (или, по другому, объем ряда распределения).
Буквой “X” принято обозначать варианту признака, а буквой f – частоту.
По своему содержанию признаки могут быть атрибутивными или количественными.
Ряды распределения построенные по атрибутивному (или качественному) признаку называются атрибутивными рядами распределения.
Например, распределение студентов по форме обучения, по факультетам, по специальностям и т.д.
Ряды распределения, построенные по количественному признаку называются вариационными рядами.
Например, распределение работников по стажу работы, по уровню заработной платы, по производительности труда и т.д.
Изучаемые в статистике признаки являются изменяющимися.
По характеру изменения (вариаций) значений признака различают:
А) признаки с прерывным изменением;
Б) признаки с непрерывным изменением.
Признаки с прерывным изменением могут принимать лишь конечное число определенных значений (например, тарифный разряд работников, количество станков и т.д.).
Признаки с непрерывным изменением могут принимать в определенных границах любые значения (например, стаж работы, размер зарплаты, пробег автотранспорта и т.п.)
По способу построения различают дискретные (прерывные) вариационные ряды, основанные на прерывной вариации признака, и интервальными(непрерывными), базирующиеся на непрерывно изменяющемся значении признака.
Статистические ряды распределения представляют собой упорядоченное распределение единиц совокупности по группам и группировкам. Ряды распределения изучают структуру совокупности, позволяют изучить ее однородность, размах и границы. Ряды распределения, образованные по качественным признакам, называют атрибутивными. При группировке по количественному признаку выделяются вариационные ряды. Вариационные ряды – ряды распределения единиц совокупности по признакам, имеющим количественное выражение, т. е. образованы численными значениями.
Вариационные ряды по строению делятся на:
- Дискретные (прерывные) – основаны на прерывных вариациях признака. Это такие ряды, где значения вариант имеют значения целых чисел (т. е. не могут принимать дробные значения). Дискретные признаки отличаются друг от друга на некоторую конкретную величину.
- Интервальные (непрерывные) – имеют любые, в том числе и дробные количественные выражения и представлены в виде интервалов. Непрерывные признаки могут отличаться один от другого на сколь угодно малую величину.
Вариационные ряды имеют два элемента:
- варианта (x)
- частота (f)
Варианта – отдельное значение варьируемого признака, которое он принимает в ряду распределения.
Частота – численность отдельных вариант или каждой группы вариационного ряда. В некоторых случаях применяется частость. Частоты, выраженные в % или долях процента, называются частостями и рссчитываются как отношение локальной частоты варианты к сумме накопленных частот.
В свою очередь, частота бывает:
- локальной
- накопленной (кумулятивная — нарастающим итогом)
Если вариационный ряд имеет неравные интервалы, то частоты в отдельных интервалах не сопоставимы, т. к. зависят от ширины интервала. В этих случаях рассчитывают плотность распределения, которая дает правильное представление о характере распределения вариант (единиц совокупности). Плотность распределения, в свою очередь, бывает:
- абсолютная плотность распределения – отношение частоты к величине (ширине) интервала
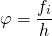
- относительная плотность распределения — отношение частости к ширине интервала
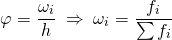
| Интервалы | Локальная частота (f) | Накопленная частота (Σf) | Частость (ω) | Плотность распределения (φ) |
| 20-30 | 0,3 | 0,03 | ||
| 30-40 | 0,5 | 0,05 | ||
| 40-50 | 0,1 | 0,01 | ||
| 50-60 | 0,1 | 0,01 |
Для характеристики рядов распределения применяются следующие показатели:
- средняя степенная
- мода
- медиана
|
|
Дата добавления: 2015-04-24; Просмотров: 2588; Нарушение авторских прав?; Мы поможем в написании вашей работы!