Точность и надежность оценок

При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, что приводит к грубым ошибкам. Поэтому в таком случае лучше пользоваться интервальными оценками, то есть указывать интервал, в который с заданной вероятностью попадает истинное значение оцениваемого параметра. Разумеется, чем меньше длина этого интервала, тем точнее оценка параметра. Поэтому, если для оценки Θ* некоторого параметра Θ справедливо неравенство | Θ* - Θ | < δ, число δ > 0 характеризует точность оценки (чем меньше δ, тем точнее оценка). Но статистические методы позволяют говорить только о том, что это неравенство выполняется с некоторой вероятностью.

Определение 18.1. Надежностью (доверительной вероятностью) оценки Θ* параметра Θ называется вероятность γ того, что выполняется неравенство | Θ* - Θ | < δ. Если заменить это неравенство двойным неравенством — δ < Θ* - Θ < δ, то получим:

p (Θ* - δ < Θ < Θ* + δ) = γ.

Таким образом, γ есть вероятность того, что Θ попадает в интервал (Θ* - δ, Θ* + δ).

Определение 18.2. Доверительным называется интервал, в который попадает неизвестный параметр с заданной надежностью γ.

45.Понятие доверительной вероятности и доверительного интервала.
Среднее арифметическое 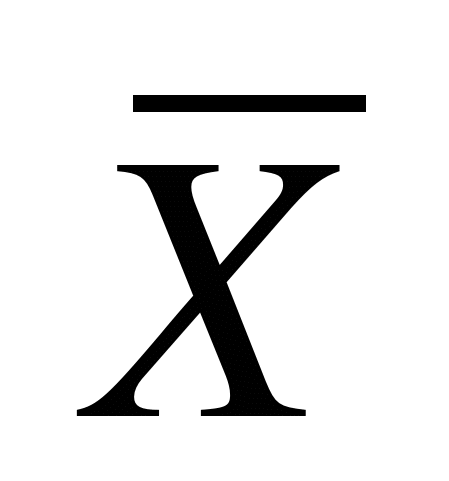является приближенной оценкой истинного значения а Dизмеряемой величины. Поэтому, чтобы эта оценка была наиболее полной, надо обязательно указать, какова погрешность полученного результата X. Величину абсолютного отклонения среднего 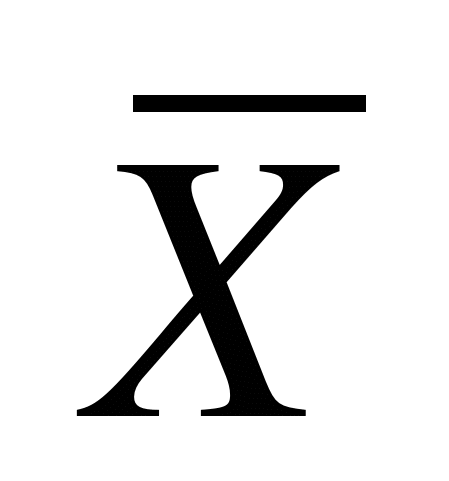из n измерений от истинного значения а называют абсолютной погрешностью или доверительным интервалом среднего. Важно не то, что в результате измерений мы получаем 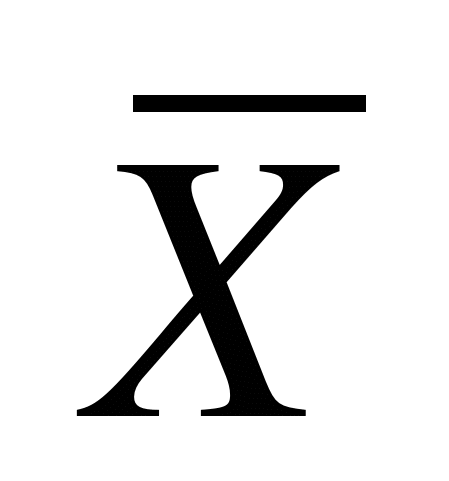, а важно то, что наряду с 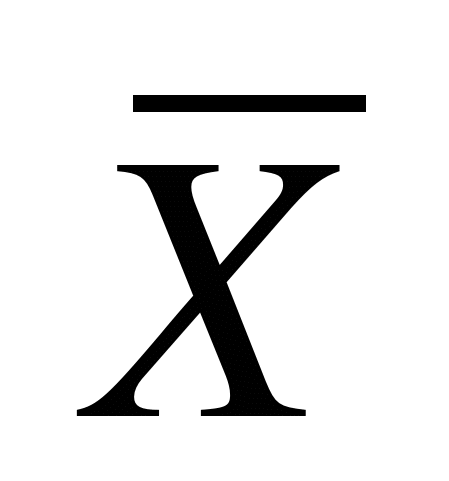Dдолжен быть указан интервал ^ X, в пределах которого где-то находится истинное значение а.

Однако мы не может достоверно утверждать, что истинное значение а окажется внутри интервала 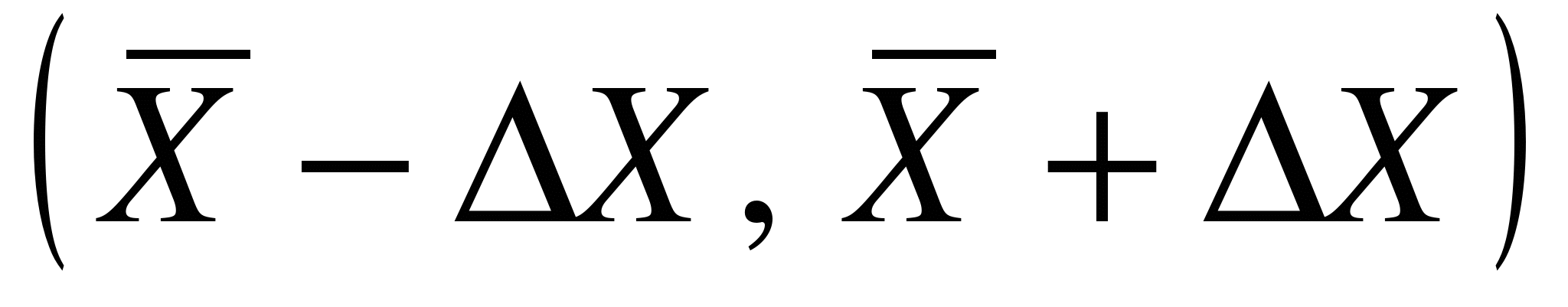D, мы можем сказать лишь следующее: имеется какая-то вероятность того, что а лежит в пределах этого интервала. Следовательно, доверительный интервал X необходимо указывать вместе с доверительной вероятностью (надежностью) a попадания истинного значения в пределы этого интервала. Без указания вероятности a Dсам по себе интервал Х не может быть принят в качестве оценки погрешности результата.
Если известен вероятностный закон распределения Р (Х), то вероятность попадания истинного значения в пределы этого интервала может быть рассчитана по формуле:

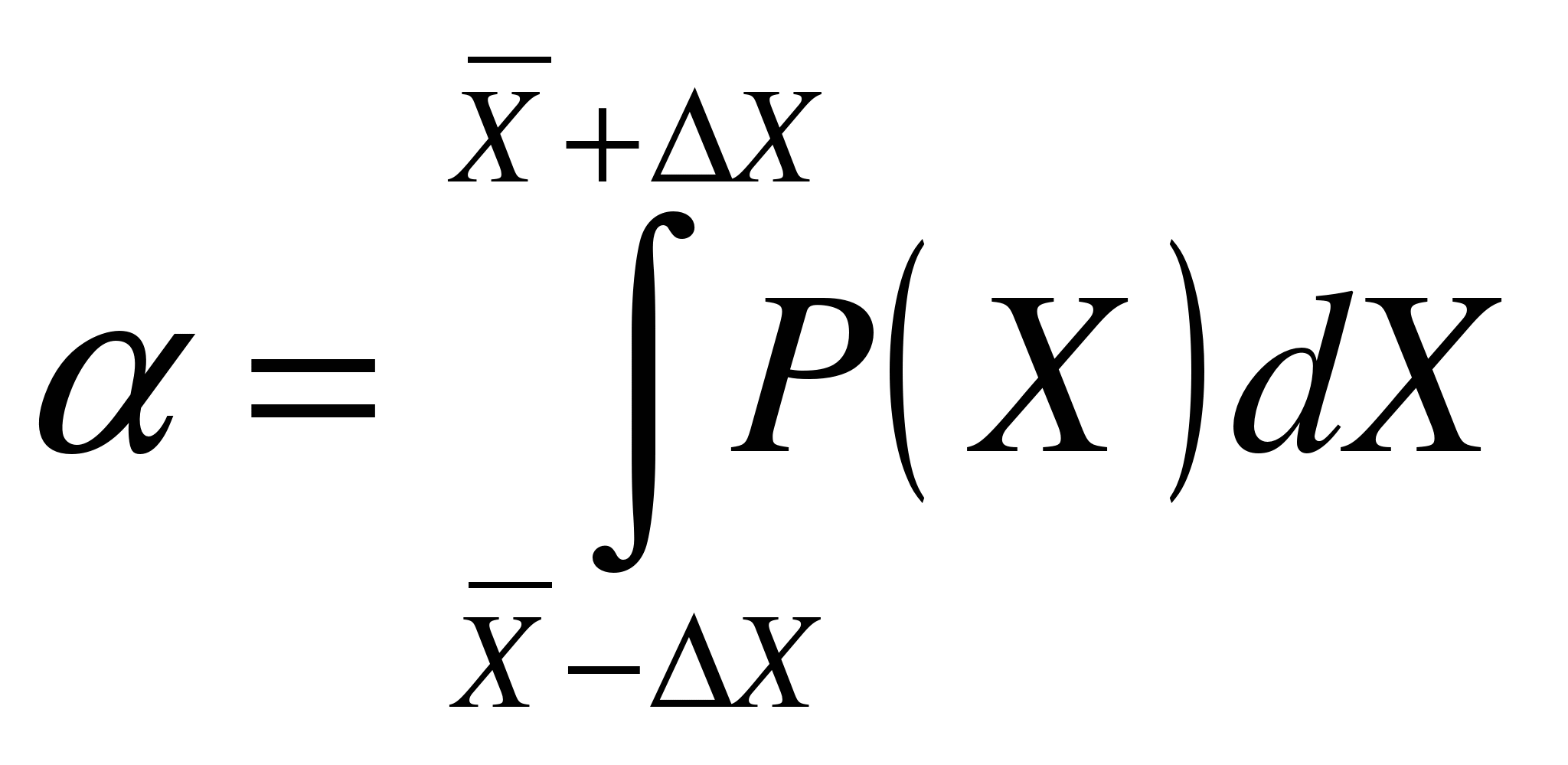(4)

Расчет показывает, что уже при числе измерений выбор погрешности 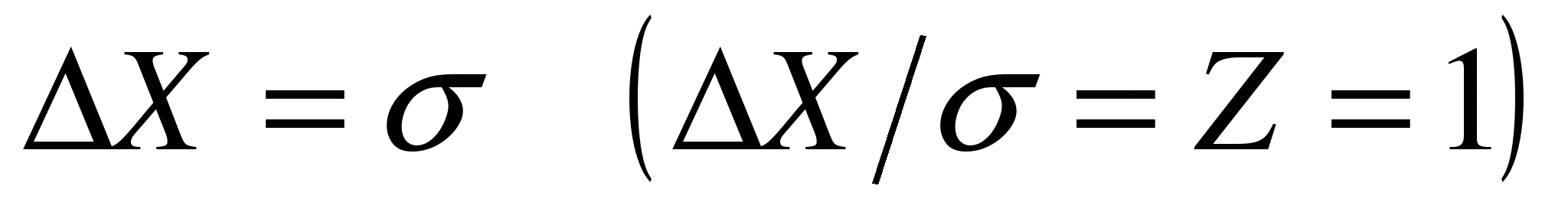, равную 0,68. Другими словами, если взять интервал надежностиa, дает величину надежности 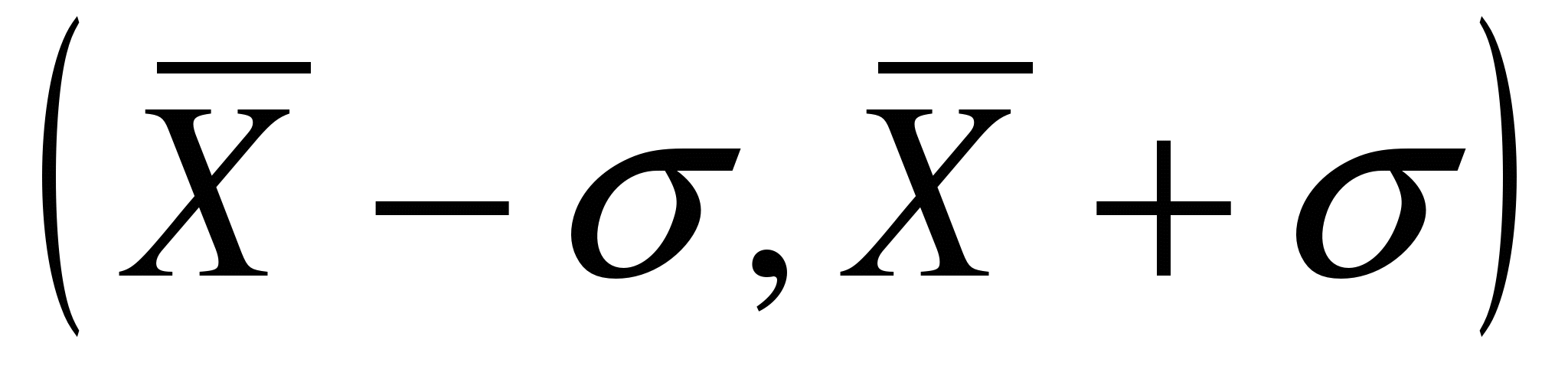, то можно утверждать, что в 68 случаях из 100 истинная величина а попадет в указанный интервал, а в 32 случаях из 100 – не попадет в этот интервал.

В случае, когда 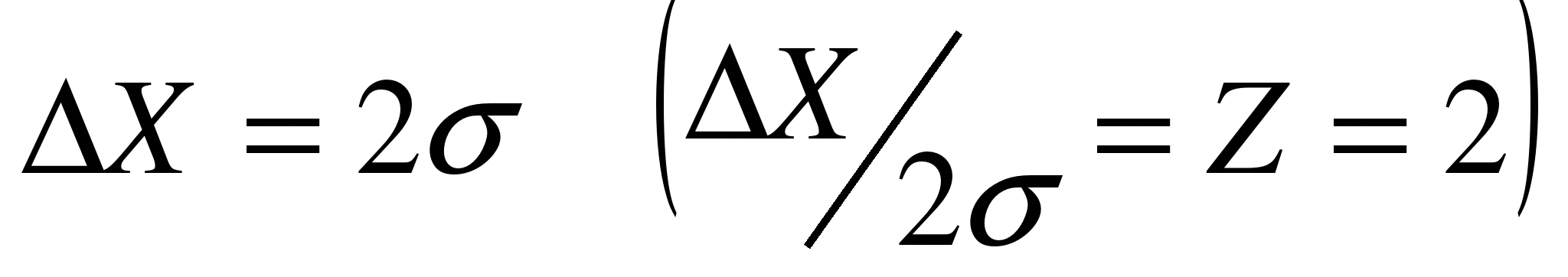, то a получается равной 0,95. Если 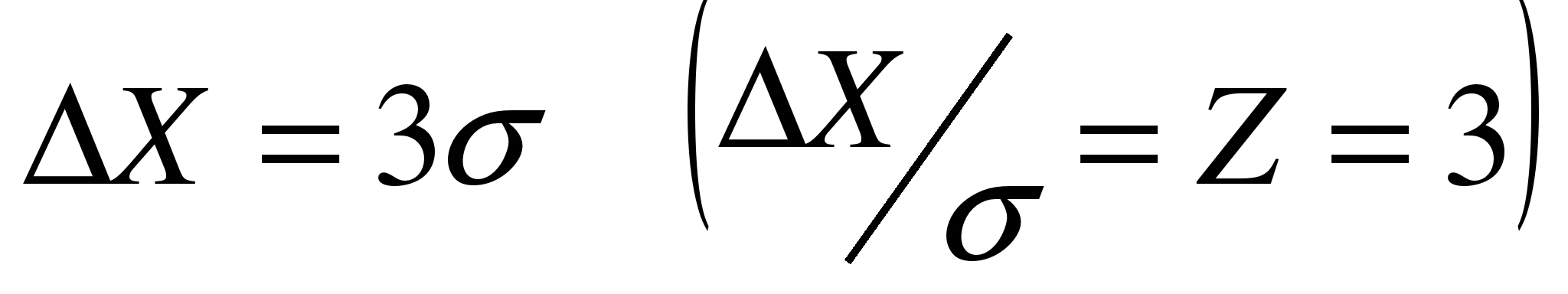, a = 0,997, т.е. за пределы доверительного интервала выйдет всего лишь около 3 измерений из 1000.

Дата добавления: 2015-04-24