Решение задачи Коши для дифференциальных уравнений методом Эйлера

Использование выборки по значимости

Очевидно, что точность вычислений можно увеличить, если область, ограничивающая искомую функцию, будет максимально к ней приближена. Для этого необходимо использовать случайные величины с распределением, форма которого максимально близка к форме интегрируемой функции. На этом основан один из методов улучшения сходимости в вычислениях методом Монте-Карло: выборка по значимости.

Метод Эйлера

Этот метод является простейшим численным методом решения задачи Коши.

Рассмотрим его на примере решения обыкновенного дифференциального уравнения первого порядка

y′ = dy(t)/dt = f (y, t)

с соответствующим начальным условием

y₀ = y(t ₀)

Заменим приращение в выражении (10.1) дифференциал dt на малое, но конечное приращение ∆t = h. Тогда соответствующее ему приращение ∆y будет равно:

∆y =h · f (t, y).

Используя начальное условие, получаем новое значение y:

y₁ = y₀ + ∆y = y₀ + h · f (t₀, y₀).

Распространяя этот подход на последующие шаги решения, получим конечно разностную формулу численного решения задачи Коши в виде:

y _i+1 = y _i + h · f (t _i, y _i).

Эта формула известна как формула метода Эйлера (часто ее называют явным методом Эйлера). Здесь (см. рис.) положение новой точки определяется по наклону кривой, вычисленному с помощью производной в данной точке. Таким образом, график численного решения представляет собой последовательность коротких прямолинейных отрезков, которыми аппроксимируется истинная кривая y = y(x). Сам численный метод определяет порядок действий при переходе от данной точки к следующей.

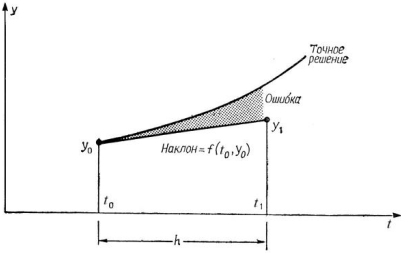
Отметим, что данную формулу можно получить, используя разложение функции y(t) в ряд Тейлора в окрестности некоторой точки t_i с последующим отбрасыванием всех членов с дифференциалами высших порядков за исключением первого. Соответственно, использование данного подхода приводит к ошибке

аппроксимации, порядок которой соответствует R_n (h²).

Несмотря на достаточно большую погрешность данного метода, его простота в сочетании с физической и математической прозрачностью обусловили его широкое применение на практике. Кроме того на базе этого метода легче понять алгоритмы функционирования более сложных методов.

В настоящее время этот метод используется при решении ряда физических задач, для которых погрешность порядка долей процента и даже нескольких процентов в ряде случаев является приемлемой. Это позволяет решать данным методом многие физические задачи достаточно просто и наглядно, попросту выбирая приемлемый для данной задачи шаг h.

Дата добавления: 2015-04-24