Решение задачи Коши для дифференциальных уравнений методом Рунге-Кутта

Метод Рунге-Кутта

Данный метод является одним из наиболее распространенных численных методов интегрирования обыкновенных дифференциальных уравнений. По сравнению с описанным выше методами Эйлера метод Рунге-Кутта имеет более

высокую точность.

Пусть на отрезке [a, b] требуется найти численное решение задачи Коши y′ = dy(t)/dt = f (y, t)

с соответствующим начальным условием

y₀ = y(t ₀)

, где a = t ₀. Как и в предыдущем методе разобьем этот участок на n равных частей и построим последовательность значений t ₀, t ₁, t ₂, …, t _n аргумента t искомой функции y(t). Предполагаем существование непрерывных производных функции y(t) до пятого порядка.

Формулу для решения можно записать в виде:

y _k+1 = y _k + ∆y _k

где ∆y _k — приращение искомой функции y(t) на (k+1)-ом шаге интегрирования.

Придадим аргументу t приращение, равное шагу интегрирования h, и разложим функцию y(t + h) в ряд Тейлора в окрестности точки t, сохранив в нем пять членов:

Перенося первое слагаемое в этой сумме в левую часть получим, что

Здесь производные определяются последовательным дифференцированием уравнения y = y (t)

Вместо непосредственных вычислений по формуле (10.6) в методе Рунге-Кутта для каждого значения ∆y _k = ∆ y(x _k) определяются четыре числа:

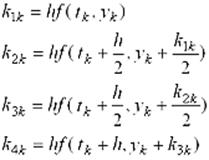
Доказывается, что если числа k 1k, k 2k, k 3k, k 4k, последовательно умножить на 1/6, 1/3, 1/3, 1/6 и сложить между собой, то выражение (10.10), соответствующее формуле Рунге-Кутта:

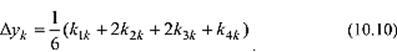
имеет погрешность R _n (h⁵).

Таким образом, рабочая формула Рунге-Кутта для интегрирования имеет вид:

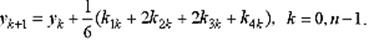
Метод Рунге-Кутта может быть использован и при решении систем дифференциальных уравнений.

Дата добавления: 2015-04-24