
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Компактные операторы. Теорема Арцелла. (док-во достаточности)
|
|
|
|
Оператор 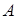 , отображающий банахово пространство
, отображающий банахово пространство 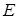 в себя (или другое банахово пространство), называется компактным (вполне непрерывным), если он каждое ограниченное множество переводит в предкомпактное.
в себя (или другое банахово пространство), называется компактным (вполне непрерывным), если он каждое ограниченное множество переводит в предкомпактное.
Теорема Арцелла: Для того, чтобы Семейство оператора A определённых на некотором отрезке [a,b] было компактным, необходимо и достаточно, чтобы этот оператор был равномерно ограниченным и равностепенно непрерывным.
Достаточность[править исходный текст]
Необходимо доказать, что равномерная ограниченность и равностепенная непрерывность семейства F влечёт существование конечной -сети для всякого конечного  .Фиксируем
.Фиксируем 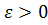 .
.
Пусть K — это константа, которая фигурирует в определении равномерной ограниченности.
Выберем такое  , которое фигурирует в определении равномерной непрерывности и соответствует величине
, которое фигурирует в определении равномерной непрерывности и соответствует величине  . Рассмотрим прямоугольник
. Рассмотрим прямоугольник  и разобьём его вертикальными и горизонтальными прямыми на прямоугольные ячейки размером меньше чем
и разобьём его вертикальными и горизонтальными прямыми на прямоугольные ячейки размером меньше чем  по горизонтали и
по горизонтали и  по вертикали. Пусть
по вертикали. Пусть 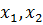 ,…,
,…,  — узлы этой решётки (по оси абсцисс).
— узлы этой решётки (по оси абсцисс).
Если рассмотреть произвольную функцию 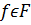 , то для каждого узла
, то для каждого узла  решётки обязательно найдётся такая точка
решётки обязательно найдётся такая точка  решётки, что
решётки, что  . Если рассмотреть ломаную функцию
. Если рассмотреть ломаную функцию  , которая в узлах принимает соответствующие значения, уклоняющиеся от функции не более чем на
, которая в узлах принимает соответствующие значения, уклоняющиеся от функции не более чем на  , то в силу того что сама функция уклоняется на каждом отрезке не более чем на
, то в силу того что сама функция уклоняется на каждом отрезке не более чем на  , ломаная на каждом таком отрезке уклоняется не более чем на
, ломаная на каждом таком отрезке уклоняется не более чем на  .
.
Поскольку каждая точка x отрезка [a,b] оказывается на одном из таких отрезков, скажем, [  ], то получается что уклонение функции от построенной таким образом ломанной не превосходит
], то получается что уклонение функции от построенной таким образом ломанной не превосходит 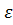 :
:
 .
.
Тем самым показано, что конечная (!) система ломанных функций указанного вида является 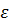 -сетью для заданного
-сетью для заданного  .
.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 523; Нарушение авторских прав?; Мы поможем в написании вашей работы!