Понятие количества информации

Информацию, которую получает человек, можно считать мерой уменьшения неопределенности знаний.

Если некоторое сообщение приводит к уменьшению неопределенности наших знаний, то можно говорить, что такое сообщение содержит информацию, и необходимости в получении дополнительной информации нет. Если после получения сообщения неопределенность осталась, значит, получена нулевая информация. Сообщения обычно содержат информацию о каких – либо событиях.

Приведенные рассуждения показывают, что между понятиями информация, неопределенность и возможность выбора существует тесная связь. Так, любая неопределенность предполагает возможность выбора, а любая информация, уменьшая неопределенность, уменьшает и возможность выбора. При полной информации выбора нет. Частичная информация уменьшает число вариантов выбора, сокращая тем самым неопределенность.

Пример. Человек бросает монету и наблюдает, какой стороной она упадет. Обе стороны монеты равноправны, поэтому одинаково вероятно, что выпадет одна или другая сторона. Такой ситуации приписывается начальная неопределенность, характеризуемая двумя возможностями. После того, как монета упадет, достигается полная ясность и неопределенность исчезает (становится равной нулю).

Приведенный пример относится к группе событий, применительно к которым может быть поставлен вопрос типа «да-нет». Количество информации, которое можно получить при ответе на вопрос типа «да-нет», называется битом (англ. bit — сокращенное от binary digit — двоичная единица). Бит — минимальная единица количества информации, ибо получить информацию меньшую, чем 1 бит, невозможно. При получении информации в 1 бит неопределенность уменьшается в 2 раза. Таким образом, каждое бросание монеты дает нам информацию в 1 бит.

Количество информации для событий с различными вероятностями определяется по формуле:

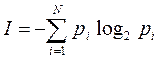, (1)

где I – количество информации

N – количество возможных событий

p_i – вероятности отдельных событий.

Если события равновероятны, то количество информации определяется по формуле:

I = log₂ N (2)

или из показательного уравнения:

N = 2^I (3)

Если количество возможных вариантов информации не является целой степенью числа 2, т.е. количество информации число вещественное, то необходимо воспользоваться калькулятором или следующей таблицей:

N	I	N	I	N	I	N	I
	0,00000		4,08746		5,04439		5,61471
	1,00000		4,16993		5,08746		5,64386
	1,58496		4,24793		5,12928		5,67243
	2,00000		4,32193		5,16993		5,70044
	2,32193		4,39232		5,20945		5,72792
	2,58496		4,45943		5,24793		5,75489
	2,80735		4,52356		5,28540		5,78136
	3,00000		4,58496		5,32193		5,80735
	3,16993		4,64386		5,35755		5,83289
	3,32193		4,70044		5,39232		5,85798
	3,45943		4,75489		5,42626		5,88264
	3,58496		4,80735		5,45943		5,90689
	3,70044		4,85798		5,49185		5,93074
	3,80735		4,90689		5,52356		5,95420
	3,90689		4,95420		5,55459		5,97728
	4,0000		5,00000		5,58496		6,00000

Единицы измерения количества информации.

Принята следующая система единиц измерения количества информации:

1 байт = 8 бит

1 Кбайт = 2¹⁰ байт = 1024 байт

1 Мбайт = 2²⁰ байт = 1024 Кбайт

1 Гбайт = 2³⁰байт = 1024 Мбайт

1 Тбайт = 2⁴⁰ байт = 1024 Гбайт

1 Пбайт = 2⁵⁰ байт = 1024 Тбайт

Определение количества информации, представленной с помощью знаковых систем.

Если рассматривать символы алфавита как множество возможных сообщений (событий) N, то количество информации, которое несет один знак, можно определить из формулы (1). Если считать появление каждого знака алфавита в тексте событиями равновероятными, то для определения количества информации можно воспользоваться формулой (2) или уравнением (3).

Количество информации, которое несет один знак алфавита, тем больше, чем больше знаков входят в этот алфавит, то есть чем больше мощность алфавита.

Количество информации, содержащейся в сообщении, закодированном с помощью знаковой системы, равно количеству информации, которое несет один знак, умноженному на число знаков в сообщении.

Дата добавления: 2015-04-24