
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Перевод чисел из одной системы счисления в другие
|
|
|
|
0, 1, 2, 3, 4, 5, 6, 7
Запись любого числа в этой системе счисления основывается на его разложении по степеням числа 8 с указанием коэффициентов.
Пример: 123,4 8=1*82+2*81 +3*80 +4*8-1=83,5 10
Для выполнения арифметических операций используются специальные таблицы.
в ) Шестнадцатеричная система счисления.
В шестнадцатеричной системе счисления используется 16 цифр. Эта система счисления отличается от остальных тем, что в ней общепринятых (арабских) цифр не хватает, поэтому вводятся новые символы. Для обозначения первых десяти чисел используются арабские цифры, от 0 до 9, а для следующих шести (от 10 до 15), используются буквенные обозначения: А - 10, В - 11, С - 12, D - 13, Е - 14, F - 15. Эта система счисления используется для записи информации в сокращенном виде. Основание q=16=24 представляет собой целую степень числа 2, благодаря этому можно так же легко перейти к двоичной системе счисления.
Запись любого числа в этой системе счисления основывается на его разложении по степеням числа 16 с указанием коэффициентов.
Пример: AF,816 = 10*161+15*160+8*161 = 175,510
а) способ подстановки степени основания.
Для перевода чисел из любой системы счисления в 10-ую систему счисления используется правило полинома: каждая Р-ичная цифра и соответствующая ей степень основания переводится в Q-ичную систему, азатем определяется значение цифры путем умножения и сложения по q-правилам, то есть любое число может быть представлено в виде:
Аq=an-1qn-1+an-2qn-2+... +a0q0+a-1q-1+... +a-mq-m
Где: |q|> = 1- основание системы счисления, в которой записано число
ai – коэффициенты
n - число целых разрядов
m - число дробных разрядов
 Пример: 1) 1101,012 ()10
Пример: 1) 1101,012 ()10
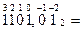 1*23+1*22+0*21+1*20+0*2-1+1*2-2=8+4+1+1/4=16,2510
1*23+1*22+0*21+1*20+0*2-1+1*2-2=8+4+1+1/4=16,2510
 2)254,38 ()10
2)254,38 ()10
 2*82+5*81+4*80+3*8-1=128+40+4+3/8=172,37510
2*82+5*81+4*80+3*8-1=128+40+4+3/8=172,37510
 3)AF,816 ()10
3)AF,816 ()10
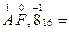 10*161+15*160+8*16-1=160+15+8/16=175,510
10*161+15*160+8*16-1=160+15+8/16=175,510
б) перевод целых чисел
Для перевода целого числа из 10-ой системы счисления в любую другую необходимо это число и получаемые целые частные последовательно делить нацело на основание системы счисления в которую переводим до получения частного меньшего основания. Число в новой системе счисления составляется из остатков и последнего частного, начиная с него.
Пример:
 1) 5410 ()2 = 110 1102
1) 5410 ()2 = 110 1102
54 | 2
54 27 | 2
0 26 13 | 2
 1 12 6 |2
1 12 6 |2
1 6 3 | 2
 0 2 1
0 2 1
 2) 34810 ()8 = 5348
2) 34810 ()8 = 5348
348 | 8
344 43 | 8
 4 40 5
4 40 5
 3
3
 3) 87510 ()16 = 36B16
3) 87510 ()16 = 36B16
875 | 16
864 54 | 16

 11 48 3
11 48 3
в) перевод дробного числа из 10 - ой системы счисления в любую другую
Для перевода последовательно умножают дробную часть числа на основание системы счисления, в которую переводим, до получения нуля в дробной части произведения или до достижения нужной степени точности. Новое число записывается как последовательность из целых частей промежуточных произведений, начиная с первого.
Пример:
 1) 0,210 ()2 = 0,001102 2) 0,72510 ()8 = 0,563148
1) 0,210 ()2 = 0,001102 2) 0,72510 ()8 = 0,563148

 0 2 0 725
0 2 0 725

 2 8
2 8
 0 4 5 800
0 4 5 800

 2 8
2 8
0 8 6 400
 2 8
2 8
 1 6 3 200
1 6 3 200
 2 8
2 8
 1 2 1 600
1 2 1 600
 2 8
2 8
 0 4 4 800
0 4 4 800
г) перевод смешанных чисел
Для перевода смешанных чисел из одной системы счисления в другую переводят отдельно целую и дробную части по известным правилам. Новое число получается соединением частей в одну запись.
Пример:
 1) 79,2510 ()2
1) 79,2510 ()2
0,2510 = 0,012
 0 25
0 25

 79 | 2 7910 10011112 2
79 | 2 7910 10011112 2
 78 29 | 2 0 50
78 29 | 2 0 50
 1 38 19 | 2 2
1 38 19 | 2 2
 1 18 9 | 2 1 00
1 18 9 | 2 1 00
1 8 4 | 2
1 4 2 | 2
 0 2 1
0 2 1
Следовательно, 79,2510 = 1001111,012
д) перевод чисел из 8,16-ой системы счисления в 2-ую систему счисления и обратно
Для перевода чисел из 2-ой систему счисления в 8-ю систему счисления двоичное число разбивается на триады (трехзначное двоичное число), а затем каждая триада заменяется соответствующей восьмеричной цифрой, используя таблицу эквивалентов. Разбиение начинают влево и вправо от запятой. Если триада неполная, то ее добавляют нулями.
 Пример: 1) 101101,012 ()8= 55,28
Пример: 1) 101101,012 ()8= 55,28
101101, 010
5 5 2
Для перевода из 8-ой системы счисления в 2-ую систему счисления каждая восьмеричная цифра заменяется соответствующей триадой двоичных цифр.
 Пример: 1267,548 ()2= 1010110111,1011002
Пример: 1267,548 ()2= 1010110111,1011002
Для перевода из 2-ой системы счисления в 16-ую систему счисления двоичное число разбивается на тетрады, которые заменяются соответствующими шестнадцатеричными цифрами.
 Пример: 001001011101, 1000 2 ()16= 25D,816
Пример: 001001011101, 1000 2 ()16= 25D,816
2 5 D 8
Для перевода из 16-ой системы счисления в 2-ую систему счисления каждая 16-ричная цифра заменяется соответствующей тетрадой двоичных цифр.
 Пример: 4AF2,5C16 ()2 = 100101011110010,010111002
Пример: 4AF2,5C16 ()2 = 100101011110010,010111002
Таблица эквивалентов
| Десятичная | Двоичная | Восьмеричная | Шестнадцатеричная | ||
| Двоичная | Двоичная | ||||
| A | |||||
| B | |||||
| C | |||||
| D | |||||
| E | |||||
| F |
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 867; Нарушение авторских прав?; Мы поможем в написании вашей работы!