Определение

Пример

Пример

А: «Выпадение не менее 2х очков при бросании кубика». B: «Выпадение не более 4х очков» Найти

ДЗ:

Пользуясь диаграммой Венна, показать справедливость формул де Моргана.

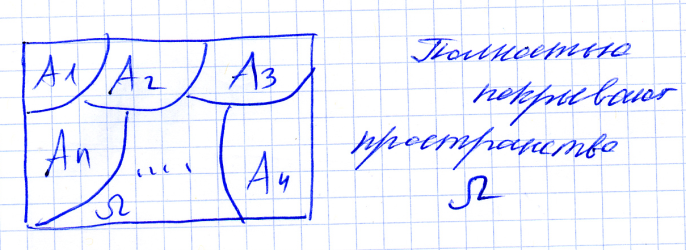
О. можно определить как систему подмножеств пространства элементарных исходов Ω, замкнутую относительно счётного числа теоретико-множественных операций.

О. Множество событий A1, A2,…An называют полной группой событий, если они попарно несовместны и появление одного и только одного из них является достоверным событием.

ВОПРОС № 2

Элементы комбинаторики. Понятие случайного события. Классическое определение вероятности.

Комбинаторика изучает способы подсчёта числа элементов в различных конечных множествах.

ШПС

ШСП

ПШС

ПСШ

СШП

СПШ

Определение

Множества элементов, состоящие из одних и тех же различных элементов и отличающиеся друг от друга только их порядком, называются перестановками этих элементов. Обозначаются перестановки P_n. P₃=6

Теорема

Число перестановок множества из n-ных элементов равно:

P_n=n! (факториал – произведение всех натуральных чисел начиная с единицы)

P_n=1∙2∙3∙…∙n

Пример:

1,2,3,4 Сколько можно составить двузначных чисел

12 13 14 21 23 24 31 32 34 41 42 43

Ответ: 12

Размещениями называют множества, выбранные из n различных элементов по k элементов, которые отличаются либо составом элементов, либо их порядком.

Обозначение:

Число размещений из n элементов по k равно:

В хоккейном турнире участвуют 6 команд. Каждая команда должна сыграть с каждой 1 игру. Сколько игр сыгранно в турнире?

Сочетаниями из n различных элементов по k называются множества, которые отличаются хотя бы одним элементом. Обозначаются сочетания

Дата добавления: 2015-04-24