Формулы и свойства степеней

Формулы и свойства степеней

Число с называется n-ной степенью числа а, если c=a•a•a•...•a

Свойства и формулы степеней используются при сокращении и упрощении сложных выражений, при решении уравнений и неравенств. Свойства степеней можно использовать совместно с таблицей степеней и таблицей умножения. В этом разделе описаны основные правила работы со степенями.

(степени с целыми показателями)

a ¹ = а, a ⁰ = 1 (a ≠ 0), a ^-n = 1/a ⁿ.

1° a ^m a ⁿ = a ^m+n;

2° a ^m /a ⁿ = a ^m-n;

3° (ab) ⁿ = a ⁿ b ⁿ;

4° (a ^m) ⁿ = a ^mn;

5° (a/b) ⁿ = a ⁿ /b ⁿ.

7 Вопрос:

Основные свойства корней.

Для любого натурального n, целого k и любых неотрицательных чисел a и b выполнены равенства:

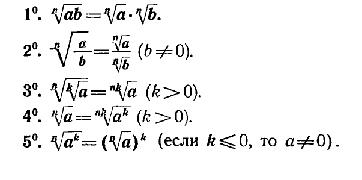
Эти пять свойств с легкостью доказываются из определения корня и степени. При решении задач, связанных с вычислением корней следует активно пользоваться жтими свойствами - они сокращают объем вычислений, позволяют упрощать выражения и оказывают другую помощь.

6°. Для любых чисел а и b, таких, что 0≤а<b, выполняется неравенство 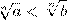. Проведем доказательство методом от противного. Допустим, что . Тогда по свойству степеней с натуральным показателем , т.е. a≥b. Это противоречит условию а<b.

8 Вопрос:

Тема урока: "Показательная функция, ее свойства и график"

Концентрация внимания:

Определение. Функция вида 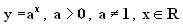называется показательной функцией.

Замечание. Исключение из числа значений основания a чисел 0; 1 и отрицательных значений a объясняется следующими обстоятельствами:

a = 0	Выражения вида 0 ^x определено при x > 0 и в этом случае тождественно равно нулю.
a = 1	Выражение 1 ^x определено при всех x, имеет постоянное значение (тождественно единице).
a < 0	Возможно возведение в целую степень или в рациональную степень с нечётным знаменателем.

Само аналитическое выражение a^x в указанных случаях сохраняет смысл и может встречаться в решении задач. Например, для выражения x^y точка x = 1; y = 1входит в область допустимых значений.

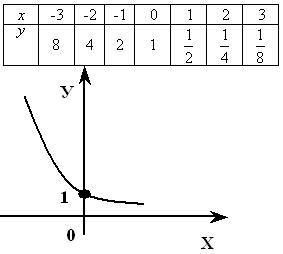
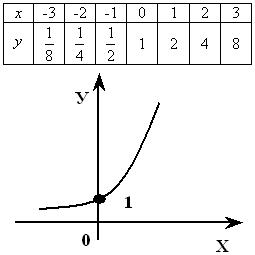
Построить графики функций: и .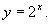

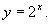
График показательной функции
y = a ^x, a > 1	y = a ^x, 0< a < 1

Дата добавления: 2015-04-24