Абсолютная и Относительная погрешности

Пусть X — точное значение некоторой величины, а х — наи­лучшее из известных приближений. В этом случае ошибка (или погрешность) приближения х определяется разностью Х- х. Обыч­но знак этой ошибки не имеет решающего значения, поэтому рассматривают абсолютную величину ошибки:

е_х=/Х-х/. (1)

Величина е_х, называемая абсолютной погрешностью приближен­ного значения х, в большинстве случаев остается неизвестной, так как для ее вычисления нужно точное значение X. Вместе с тем на практике обычно удается установить верхнюю границу абсо­лютной погрешности, т.е. такое (по возможности наименьшее) число? x, для которого справедливо неравенство

? x? /Х-х/. (2)

Число? x в этом случае называют предельной абсолютной по­грешностью (или границей абсолютной погрешности) приближения х.

Таким образом, предельная абсолютная погрешность прибли­женного числа х — это всякое число? x, не меньшее абсолютной погрешности е_х этого числа.

Пример 1. Возьмем число? = 3,14159265358.... Если вызвать? на индикатор 8-разрядного МК, получим приближение этого чи­сла:

?’ = 3,1415926.

Попытаемся выразить абсолютную погреш­ность значения?':

е _?' =/?-?'/ =0,00000005358....

Получили беско­нечную дробь, непригодную для практических расчетов. Очевид­но, однако, что е _?' < 0,00000006, следовательно, число 0,00000006 = 0,6*10^-7 можно считать предельной абсолютной погрешностью приближения, используемого МК вместо числа е _?' :?? ' = 0,6*10^-7.

Неравенство (2) позволяет установить приближения к точ­ному значению X по недостатку и избытку:

х -? x < X < х +? x, (3)

которые могут рассматриваться как одна из возможных пар значе­ний соответственно нижней границы (НГ) и верхней границы (ВГ) приближения х:

НГ_х=х-? x; ВГ_х=х +? x. (4)

Во многих случаях значения границы абсолютной ошибки? x, так же как и наилучшие значения приближения х, получаются на практике в результате измерений. Пусть, к примеру, в результате повторных измерений одной и той же величины получены значе­ния: 5,2; 5,3; 5,4; 5,3. В этом случае естественно принять за наилуч­шее приближение измеряемой величины среднее значение х= 5,3. Очевидно также, что граничными значениями величины х в дан­ном случае будут НГ_Х = 5,2, ВГx= 5,4, а граница абсолютной по­грешности? x может быть определена как половина длины интер­вала, образуемого граничными значениями НГx и ВГ_Х, т.е.

? x =(5,4-5,2)/2=0.1

По абсолютной погрешности нельзя в полной мере судить о точности измерений или вычислений. Качество приближения из­меряется с помощью относительной погрешности, которая опре­деляется как отношение ошибки е_х к модулю значения X (когда оно неизвестно, то к модулю приближения х).

Предельной относительной погрешностью (или границей отно­сительной погрешности)?х приближенного числа называется от­ношение предельной абсолютной погрешности к абсолютному значению приближения х:

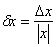. (5)

Формула (5) позволяет при необходимости выражать абсо­лютную погрешность через относительную:

?x = |х|?х. (6)

Относительную погрешность выражают обычно в процентах.

Пример 2. Вычислить границу относительной погрешности приближения к числу?, используемого 8-разрядным МК.

Учитывая, что 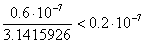можно принять??’= 0,000002%.

Это чрезвычайно высокая точность, если учесть, что для ординарных технических расчетов считается приемлемым уро­вень точности от 0,1 до 5%.

Дата добавления: 2015-04-24