
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Абсолютная и относительная погрешности
|
|
|
|
Пример 3.
Пример 2.
Пример 1.
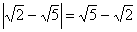 , т.к.
, т.к. 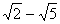 < 0;
< 0;
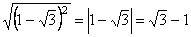 , т.к.
, т.к. 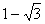 < 0
< 0
Упростить выражение 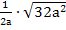 , если a < 0.
, если a < 0.
Решение.

Так как по условию а < 0, то |а| = -а. В результате получаем
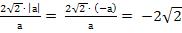
Ответ: 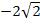
Вычислить
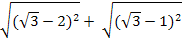
Решение.
Имеем
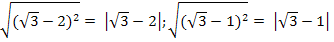
Теперь раскроем знаки модулей.
Воспользуемся тем, что 1 < √ 3 < 2. Значит, √3 - 2 < 0, а √3 - 1 > 0.
Но тогда |√3 - 2| = -(√3 - 2) = 2- √3,
а |√3 - 1| = √3 - 1
В итоге получаем
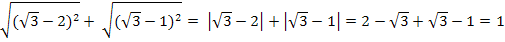
5 Вопрос:
Анализ погрешностей является неотъемлемой частью процесса решения прикладной задачи. Часть этих погрешностей связана с вычислениями, которые в наше время производятся на ЭВМ. С увеличением скорости производства вычислений и с вовлечением в счетный процесс чисел с большим количеством значащих цифр, как это делается в ЭВМ, потребность в оценке фактической точности результата лишь возрастает. Задача анализа погрешностей сводится, по существу, к отысканию их надежных границ и к соблюдению условий, обеспечивающих их минимальное распространение.
Возникновение, накопление и распространение ошибок проходят через все стадии решения прикладной задачи, начиная с получения значений исходных данных.
На общую погрешность задачи, как это уже отмечалось, влияет целый ряд факторов. Отметим основные из них, рассмотрев общий ход решения задачи — от построения математической модели до производства вычислений.
Пусть R — точное значение результата решения некоторой задачи. Из-за несоответствия построенной математической модели реальной ситуации, а также по причине неточности исходных данных вместо R будет получен результат, который обозначим R1. Образовавшаяся таким образом погрешность?1 = R – R1уже не может быть устранена в ходе последующих вычислений (так называемая неустранимая погрешность).
Приступив к решению задачи в рамках математической модели, мы избираем приближенный (например, численный) метод и, еще не приступив к вычислениям, допускаем новую погрешность, приводящую к получению результата R2 (вместоR1 ). Погрешность?2 = R2 – R1называют погрешностью метода.
Действия над числами вносят дополнительную погрешность. Например, если складывать два числа с одинаковыми погрешностями, то погрешность суммы будет, вообще говоря, больше погрешности каждого из слагаемых. Это обстоятельство, а также неизбежность округлений (в случае использования ЭВМ принудительное округление диктуется конечностью разрядной сетки машины) приводят к получению результата R3,отличающегося от R2 на величину вычислительной погрешности?3 = R3 – R2.Полная погрешность?, очевидно, получается как сумма всех погрешностей:
? = R - R3 = (R – R1) + (R1 - R2) + (R2 – R3) =?1 +?2 +?3.
При решении конкретных задач те или иные виды погрешностей могут отсутствовать или незначительно влиять на окончательный результат. Тем не менее, для исчерпывающего представления о точности окончательного результата в каждом случае необходим полный анализ погрешностей всех видов. Это в полной мере относится и к неустранимой погрешности — погрешности математической модели. Располагая несовершенной математической моделью, вычислитель должен каким-то способом составить представление о величине неустранимой погрешности. Понятно, что в условиях слишком грубой модели не имеет смысла проводить утонченный анализ вычислительных ошибок. Отсюда следует, что оценка неустранимой погрешности может послужить веским доводом для снижения требований к точности последующих вычислений, что, в свою очередь, может сделать их менее трудоемкими.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 925; Нарушение авторских прав?; Мы поможем в написании вашей работы!