Умножение комплексных чисел

Сложение и вычитание

Преобразование десятичной дроби в обыкновенную дробь

Сравнение дробей

Деление дробей

Умножение дробей

Чтобы умножить две обыкновенные дроби, нужно перемножить их числители и знаменатели:

	·		=	3 · 2	=
		7 · 5

Чтобы умножить дробь на натуральное число, надо числитель умножить на число, а знаменатель оставить тем же:

	· 2	=	3 · 2	=

Упражнения на тему умножение двух дробей.

Чтобы получить дробь, обратную данной, следует поменять местами числитель и знаменатель. Чтобы разделить одну обыкновенную дробь на другую, надо умножить первую дробь на дробь, обратную второй:

	:		=		·		=	3 · 5	=
				7 · 4

Упражнения на тему деление двух дробей.

Из двух дробей с одинаковыми знаменателями больше та дробь, числитель которой больше.

	<

Из двух дробей с одинаковыми числителями больше та дробь, знаменатель которой меньше.

	>

Чтобы сравнить две обыкновенные дроби, следует привести дроби к общему знаменателю и сравнить числители получившихся дробей. Дробь с большим числителем будет больше.
Например:

	?

приведем дроби к общему знаменателю

	?

так как 60 < 63, то

	<

Упражнения на тему сравнение двух дробей.

Чтобы преобразовать десятичную дробь в дробь обыкновенную, следует представить её дробную часть в виде натурального числа, делённого на 10 в соответствующей степени. Затем упростить получившуюся дробь и к результату приписать целую часть со знаком, формируя смешанную дробь.
Например:

1.346	= 1		= 1

3 Вопрос:

По аналогии со сложением и вычитанием векторов мы приходим к следующему правилу сложения и вычитания комплексных чисел:

(a ₁ + b ₁ i) + (a ₂ + b ₂ i) +...+ (a_n + b_ni) = (a ₁ + a ₂ +...+ a_n) + (b ₁+ b ₂+...+ b _n) i = a + bi

Операция введена, так как получили элемент того же множества.

Вычитание определяется как действие, обратное сложению, то есть разность x + iy = (a ₁ + b ₁ i) – (a ₂ + b ₂ i) определяется из условия:

(x + iy) + (a ₂ + b ₂ i) = (a ₁ + b ₁ i).

Из правила сложения получаем:

x + a ₂ = a ₁,
y + b ₂ = b ₁.

То есть x = a ₁ – a ₂, y = b ₁ – b ₂ и разность

(a ₁ + b ₁ i) – (a ₂ + b ₂ i) = (a ₁ – a ₂) + (b ₁ – b ₂) i.

Определение. Произведением двух комплексных чисел называется такое комплексное число, модуль которого равен произведению модулей сомножителей, а аргумент – сумме аргументов сомножителей.

Это определение совершенно очевидно, если использовать показательную форму комплексного числа:

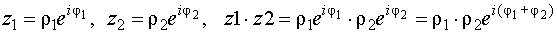
Пусть комплексные числа даны в алгебраической форме. Найдём их произведение: (a ₁ + b ₁ i) (a ₂ + b ₂ i) = x + iy.

Имеем .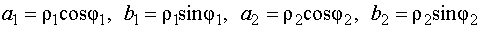

Согласно определению умножения можем записать:

.

Распишем: ,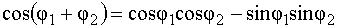

,

.

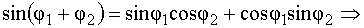
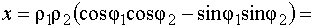
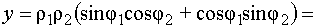
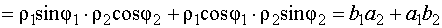Окончательно получим:

.

Отсюда следует правило умножения комплексных чисел в алгебраической форме: комплексные числа можно перемножать как многочлены.

Если z = а + b i – комплексное число, то число 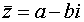называется сопряжённым с числом z. Его обозначают при помощи черты над числом.

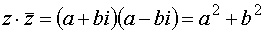, но , следовательно, .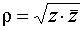

Дата добавления: 2015-04-24