Дифференциальное уравнение свободных гармонических колебаний и его решение

Кваизиупругая сила, ее физический смысл, вид. Дифференциальное уравнение свободных гармонических колебаний и его решение. Собственная частота различных осцилляторов.

Квазиупр у гая с и ла, направленная к центру О сила F, величина которой пропорциональна расстоянию r от центра О до точки приложения силы; численно F = cr, где с — постоянный коэффициент. Тело, находящееся под действием К. с., обладает потенциальной энергией П = ¹/₂ cr ². Название "К. с." связано с тем, что аналогичным свойством обладают силы, возникающие при малых деформациях упругих тел (так называемые силы упругости). Для материальной точки, находящейся под действием К. с., центр О является положением устойчивого равновесия. Выведенная из этого положения точка будет совершать около О линейные гармонические колебания или описывать эллипс (в частности, окружность).

F = m·a = - m· w ²·х = - k·x,

где k - постоянная величина.

Итак, тело совершает гармонические колебания, если сила, возвращающая его в положение равновесия, пропорциональна смещению и направлена в противоположную этому смещению сторону.
Такая сила называется квазиупругой.

дает зависимость колеблющейся величины S от времени t; это и есть уравнение свободных гармонических колебаний в явном виде. Однако обычно под уравнением колебаний понимают иную запись этого уравнения, в дифференциальной форме. Возьмем для определенности уравнение (1) в виде

дважды продифференцируем его по времени:

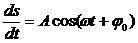
Видно, что выполняется следующее соотношение:

⁽²⁾

которое и называется уравнением свободных гармонических колебаний (в дифференциальной форме). Уравнение (1) является решением дифференциального уравнения (2). Поскольку уравнение (2) - дифференциальное уравнение второго порядка, необходимы два начальных условия для получения полного решения (то есть определения входящих в уравнение (1) констант A и j₀); например, положение и скорость колебательной системы при t = 0.

Дата добавления: 2015-04-24