Гармонические колебания в электромагнитном контуре. Дифференциальное уравнение, период и частота собственных колебаний. Волновое сопротивление. Электромеханическая аналогия

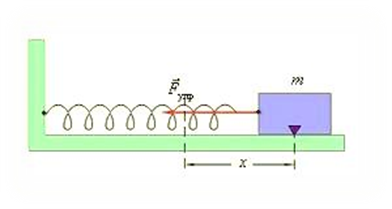
Энергия гармонического колебательного движения. Кинетическая, потенциальная, полная энергия. Среднее значение кинетической и потенциальной энергии. Интенсивность.

Потенциальная энергия:

значит 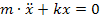и

Учитывая, что и получим:

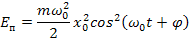
Кинетическая энергия:

Тогда, энергия гармонического колебательного движения:

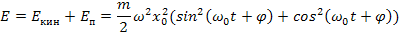
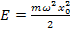т.е. полная энергия не меняется со временем и в каждой точке колебания равна начальной.

Cреднее значение кинетической энергии:

Интенсивность колебаний - средняя энергия колебаний за период. Интенсивность пропорциональна квадрату амплитуды. Или Интенсивность колебаний I - средняя энергия колебаний за период.

1) Электромагнитные колебания — это колебания электрических и магнитных полей, которые сопровождаются периодическим изменением заряда, тока и напряжения.

2)ДУ, период,частота собственных колебаний.

ДУ:

Период: (Формула Томпсона)

Частота:

Волновое сопротивление:

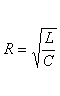
4)Электромеханическая аналогия.

Смещение х-------------------------->заряд q

скорость v----------------------------->cила тока I

масса m-------------------------------->индуктивность L

коэффициент жесткости к------->обр. емкость 1/С

потенц.энергия (кх^2)/2---------->энергия конденсатора q^2/(2C)

кин.энергия (mv^2)/2-------------->энергия катушки(LI^2)/2

коэф. Сопротивления r------------>активное сопротивление R

13. Затухающие колебания. Дифференциальное уравнение затухающих колебаний и его решение. Характеристики: амплитуда, время релаксации, декремент затухания, добротность.

Затухающие колебания – колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшаются. Простейшим механизмом уменьшения энергии колебаний является ее превращение в теплоту вследствие трения в механических колебательных системах, а также омических потерь и излучения электромагнитной энергии в электрических колебательных системах.

Дифференциальное уравнение свободных затухающих колебаний линейной системы задается в виде

(1.1)

где s – колеблющаяся величина, описывающая тот или иной физический процесс, d=const — коэффициент затухания, w0 — циклическая частота свободных незатухающих колебаний той же колебательной системы, т. е. при d=0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы.

Решение уравнения рассмотрим в виде 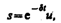(1.2)

где u=u(t). После нахождения первой и второй производных выражения (1.2) и подстановки их в (1.1) получим 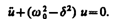(1.3)

Решение уравнения (1.3) зависит от знака коэффициента перед искомой величиной. Рассмотрим случай, когда этот коэффициент положителен: (1.4)

(если (w0² - б²)>0, то такое обозначение мы вправе сделать). Тогда получим уравнение типа (142.1) ü+w2и=0, решением которого является функция и=А0cos(wt+j). Таким образом, решение уравнения (1.1) в случае малых затуханий (б²<<w0²)

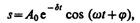(1.5)

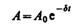где (1.6)

— амплитуда затухающих колебаний, а А0 — начальная амплитуда. Зависимость (146.5) показана на рис. 208 сплошной линией, а зависимость (1.6) — штриховыми линиями. Промежуток времени t=1/d, в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации.

Затухание нарушает периодичность колебаний, поэтому затухающие колебания не являются периодическими и, строго говоря, к ним неприменимо понятие периода или частоты. Однако если затухание мало, то можно условно пользоваться понятием периода как промежутка времени между двумя последующими максимумами (или минимумами) колеблющейся физической величины. Тогда период затухающих колебаний с учетом формулы (1.4) равен

Если A(t) и А(t + Т) — амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение

называется декрементом затухания, а его логарифм

(1.7)

— логарифмическим декрементом затухания; Ne — число колебаний, совершаемых за время уменьшения амплитуды в е раз. Логарифмический декремент затухания — постоянная для данной колебательной системы величина.

Для характеристики колебательной системы пользуются понятием добротности Q, которая при малых значениях логарифмического декремента равна

(1.8)

(так как затухание мало (б²<<w0²), то T принято равным Т0).

Из формулы (1.8) следует, что добротность пропорциональна числу колебаний Ne, совершаемых системой за время релаксации.

Дата добавления: 2015-04-24