Адиабатический процесс. Уравнение Пуассона. График адиабатического процесса

Адиабатическим называется процесс, при котором отсутствует теплообмен (dQ=0) между системой и окружающей средой. К адиабатическим процессам можно отнести все быстропротекающие процессы. Например, адиабатическим процессом можно считать процесс распространения звука в среде, так как скорость распространения звуковой волны настолько велика, что обмен энергией между волной и средой произойти не успевает. Адиабатические процессы применяются в двигателях внутреннего сгорания (расширение и сжатие горючей смеси в цилиндрах), в холодильных установках и т. д.

Из первого начала термодинамики (dQ=dU+dA) для адиабатического процесса следует, что (1)

т. е. внешняя работа совершается за счет изменения внутренней энергии системы.

Используя выражения (1) для произвольной массы газа перепишем уравнение (1) в виде (2)

Продифференцировав уравнение состояния для идеального газа получим

(.3)

Исключим из (2) и (3) температуру Т.

Разделив переменные и учитывая, что Сp/СV=g найдем

Интегрируя это уравнение в пределах от p1 до p2 и соответственно от V1 до V2, а затем потенцируя, придем к выражению

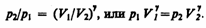
Так как состояния 1 и 2 выбраны произвольно, то можно записать

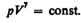(4)

Полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.

Для перехода к переменным Т, V или p, Т исключим из (55.4) с помощью уравнения Клапейрона — Менделеева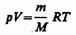

соответственно давление или объем: (5)

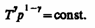(6)

Выражения (4) — (6) представляют собой уравнения адиабатического процесса. В этих уравнениях безразмерная величина

(7)

называется показателем адиабаты (или коэффициентом Пуассона). Для одноатомных газов (Ne, He и др.), достаточно хорошо удовлетворяющих условию идеальности, i=3, g=1,67. Для двухатомных газов (Н2, N2, О2 и др.) i=5, g=1,4. Значения g, вычисленные по формуле (7), хорошо подтверждаются экспериментом.

Диаграмма адиабатического процесса (адиабата) в координатах р, V изображается гиперболой (рис. 83). На рисунке видно, что адиабата (pVg = const) более крута, чем изотерма (pV = const). Это объясняется тем, что при адиабатическом сжатии 1—3 увеличение давления газа обусловлено не только уменьшением его объема, как при изотермическом сжатии, но и повышением температуры.

Дата добавления: 2015-04-24