Вывод основного уравнения МКТ. Физический смысл термодинамической температуры. Среднеквадратичная скорость. Средняя энергия поступательного движения молекул газа

Атомно-молекулярное строение вещества. Термодинамический и молекулярно-кинетический подходы к изучению вещества. Равновесное состояние. Термодинамичесике параметры. Модель идеального газа. Уравнение состояния идеального газа.

Для большинства веществ частицы представляют собой молекулы. Молекула — наименьшая частица вещества, обладающая его химическими свойствами. Молекулы в свою очередь состоят из атомов. Атом — наименьшая частица элемента, обладающая его химическими свойствами.

Термодинамика изучает свойства макроскопических систем и протекающие в них процессы, не вдаваясь в микроскопическую природу тел.

Основные положения молекулярно-кинетической теории заключаются в следующем:

все тела в природе состоят из мельчайших частиц (атомов и молекул). Наши органы чувств воспринимают их как сплошные или непрерывные;

эти частицы находятся в непрерывном хаотическом движении;

между частицами вещества существуют силы притяжения и отталкивания, зависящие от расстояния между частицами.

Термодинамическая система может находиться в различных состояниях, отличающихся температурой, давлением, объемом, плотностью и т.д. Подобные величины, характеризующие состояние системы, называются параметрами состояния.

Состояние термодинамической системы будет равновесным, если все параметры состояния имеют равные значения для любых областей системы, не изменяющиеся с течением времени, т.е. сохраняющиеся бесконечно долго при неизменных внешних воздействиях.

Сначала рассмотрим самую простую модель термодинамической системы – идеальный газ. В модель идеального газа заложено два основных предположения: первое – о невзаимодействии молекул газа на расстоянии (взаимодействие осуществляется только в пренебрежимо краткое по сравнению со временем полета время соприкосновения), и второе – о возможности пренебрежения собственным объемом молекул по сравнению с полным объемом, занимаемым газом. Эта модель хорошо себя оправдывает в случае достаточно разреженных газов, когда диаметр молекул много меньше среднего расстояния между ними. Разумеется, применимость модели идеального газа не безгранична, и имеется достаточно много явлений (например, фазовые превращения – переход из одного агрегатного состояния в другое), для анализа которых даже на качественном уровне модель идеального газа непригодна и, значит, в этих случаях следует обращаться к более сложным моделям. Уравнение состояния идеального газа в расчете на один моль принимает вид

РV = RT

Пусть имеется кубический сосуд с ребром длиной и одна частица массой в нём.

Обозначим скорость движения , тогда перед столкновением со стенкой сосуда импульс частицы равен , а после — 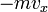, поэтому стенке передается импульс . Время, через которое частица сталкивается с одной и той же стенкой, равно .

Отсюда следует:

Так как давление , следовательно сила

Подставив, получим:

Преобразовав:

Так как рассматривается кубический сосуд, то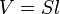

Отсюда:

.

Соответственно, и .

Таким образом, для большого числа частиц верно следующее: , аналогично для осей y и z.

Поскольку , то . Это следует из того, что все направления движения молекул в хаотичной среде равновероятны.

Отсюда

или .

Пусть — среднее значение кинетической энергии всех молекул, тогда:

, откуда, используя то, что 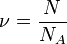(количество вещества), а , имеем .

Абсолютная термодинамическая температура — Хаотическое тепловое движение на плоскости частиц газа таких как атомы и молекулы.

Уравнение среднеквадратичной скорости молекулы

Уравнение среднеквадратичной скорости молекулы легко выводится из основного уравнения МКТ для одного моля газа.

,

, где 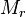— молярная масса газа

Отсюда окончательно

Дата добавления: 2015-04-24