Вектор Пойнтинга

ОСНОВНЫЕ УРАВНЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

Все электрически заряженные частицы окружены электромагнитным полем, составляющим с ними единое целое. Но- электромагнитное поле может существовать и в свободном, отдельном от заряженных частиц состоянии в виде движущихся со скоростью света фотонов или излученного, движущегося с этой скоростью электромагнитного поля. Последнее характеризуется непрерывным его распределением в пространстве и является носителем определенного количества энергии, которая способна преобразовываться в другие виды ее.

Из основ электротехники известно, что в электромагнитной волне, свободно распространяющейся в однородном и изотропном диэлектрике, векторы Е и Н взаимно перпендикулярны; энергии магнитного и электрического полей прямой или обратной волны равны. Энергия электрического и магнитного полей, заключенная в объеме V, изменяется во времени:

Этот вектор имеет размерность мощности (энергии в единицу времени), передаваемой сквозь единицу поверхности, нормальной к направлению распространения волны, и определяется следующим соотношением:

(в системе СИ),

где E и H — векторы напряжённости электрического и магнитного полей соответственно

Этот вектор по модулю равен количеству энергии, переносимой через единичную площадь, нормальную к S, в единицу времени. Своим направлением вектор определяет направление переноса энергии.

13.Уравне́ния Ма́ксвелла — система дифференциальных уравнений, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах. Вместе с выражением для силы Лоренца образуют полную систему уравнений классической электродинамики.

Название	СГС	СИ
Закон Гаусса
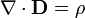
Закон Гаусса для магнитного поля
Закон индукции Фарадея
Теорема о циркуляции магнитного поля

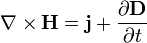
Жирным шрифтом в дальнейшем обозначаются векторные величины, курсивом — скалярные.

Введённые обозначения:

§ — плотность стороннего электрического заряда (в единицах СИ — Кл/м³);

§ — плотность электрического тока (плотность тока проводимости) (в единицах СИ — А/м²); в простейшем случае - случае тока, порождаемого одним типом носителейзаряда, она выражается просто как , где — (средняя) скорость движения этих носителей в окрестности данной точки, ρ₁ - плотность заряда этого типа носителей (она в общем случае не совпадает с ρ)^[29]; в общем случае это выражение надо усреднить по разным типам носителей;

§ — скорость света в вакууме (299 792 458 м/с);

§ — напряжённость электрического поля (в единицах СИ — В/м);

§ — напряжённость магнитного поля (в единицах СИ — А/м);

§ — электрическая индукция (в единицах СИ — Кл/м²);

§ — магнитная индукция (в единицах СИ — Тл = Вб/м² = кг•с⁻²•А⁻¹);

§ — дифференциальный оператор набла, при этом:

означает ротор вектора,

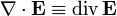означает дивергенцию вектора.

Приведённые выше уравнения Максвелла не составляют ещё полной системы уравнений электромагнитного поля, поскольку они не содержат свойств среды, в которой возбуждено электромагнитное поле. Соотношения, связывающие величины , , , и и учитывающие индивидуальные свойства среды, называются материальными уравнениями.

Дата добавления: 2015-04-24