Напряженность электрического поля. Поле точечного заряда и сферы

Если в пространство, окружающее электрический заряд, внести другой заряд, то на него будет действовать кулоновская сила, следовательно, в пространстве, окружающем электрические заряды, существует силовое поле.

Электрическое поле — поле, посредством которого взаимодействуют электрические заряды. Поля, которые создаются неподвижными электрическими зарядами и называются электростатическими.

Пробный точечный положительный заряд — такой заряд, который не искажает исследуемое поле (не вызывает перераспределения зарядов, создающих поле)

Напряженность электростатического поля в данной точке есть физическая величина, определяемая силой, действующей на пробный единичный положительный заряд, помещенный в эту точку поля:

Единица потока вектора напряженности электростатического поля — вольтметр (В • м)

Пусть поле создано точечным зарядом q. Определим напряженность поля в точке М, находящейся на расстоянии r от заряда (рис. 6). Поместим в эту точку пробный положительный заряд q ₀. Тогда, согласно закону Кулона, на заряд q ₀ со стороны заряда q действует сила, модуль которой .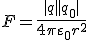

Рис. 6

Согласно определению, модуль напряженности поля в точке Μ

Если заряд q находится в среде с диэлектрической проницаемостью ε, то модуль напряженности поля, создаваемого пробным зарядом q на расстоянии r от него, составляет

Направление вектора напряженности в точке Μ поля зависит от знака заряда, создающего это поле, и сонаправлено с силой, действующей на заряд q ₀ (рис. 7, а, б). Можно связать направление вектора напряженности с направлением радиуса-вектора точки М. Если заряд, создающий поле, q > 0, то 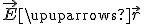, т.е. напряженность направлена от заряда, создающего поле. Если же q < 0, то 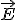направлена навстречу 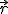, т. е. к заряду, создающему поле:

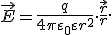
Рис. 7

По этой формуле можно рассчитывать напряженность поля, образованного заряженной проводящей сферой, в точках, находящихся на поверхности сферы и вне ее. Внутри же проводящей сферы Е = 0. Таким образом, (если r ≥ R), Е = 0 (если r < R), где R — радиус сферы.

3 Линии напряженности электрического поля. Поток вектора напряженности. Теоремы Остроградского – Гаусса. Поле бесконечной однородно заряженной плоскости и двух параллельных разноименно заряженных плоскостей.

Линией напряженности электрического поля называется линия, касательная к которой в каждой точке совпадает с вектором напряженности

Линии напряженности электростатического поля начинаются на положительных электрических зарядах и кончаются на отрицательных электрических зарядах или уходят в бесконечность.

Распределение линий напряженности вокруг точечного заряда показано на рис. 106 а, б.

Определяя направление вектора в различных точках пространства, можно представить картину распределения линий напряженности электрического поля.

Для двух одноименных зарядов эта картина имеет вид, показанный на рис. 107, для разноименных — на рис. 108.

Чтобы с помощью линий напряженности можно было характеризовать не только направление, но и значение напряженности электростатического поля, условились проводить их с определенной густотой (рис. 122): число линий напряженности, пронизывающих единицу площади поверхности, перпендикулярную линиям напряженности, должно быть равно модулю вектора Е. Тогда число линий напряженности, пронизывающих элементарную площадку dS, нормаль пк которой образует угол а с вектором Ё, равно EdScos a ~ EndS, где Еп— проекция вектора Ё на нормаль п к площадке с!5'(рис. 123). Величина называется потоком вектора напряженности сквозь площадку dS. Здесь &S = dSn — вектор, модуль которого равен dS, а направление совпадает с направлением нормали п к площадке. Выбор направления вектора п (а следовательно, и dS) условен, так как его можно направить в любую сторону.

ИЛИ (Введем понятие потока N вектора напряженности 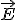сквозь некоторую поверхность площадью S. Пусть плоская поверхность площадью S находится в однородном электростатическом поле 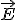(рис. 1). Вектор 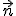— нормаль к поверхности. Угол между направлением линий напряженности и нормалью равен α. Потоком N вектора напряженности 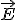через поверхность площадью S называют физическую скалярную величину, определяемую выражением

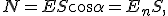
где E _n — проекция вектора 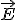на направление нормали .

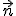Рис. 1

Так как густота линий напряженности характеризует модуль напряженности E, то можно сказать, что поток вектора напряженности через данную поверхность равен полному числу линий напряженности, проходящих через эту поверхность.

Если поле неоднородно, а поверхность не является плоской, то в этом случае для определения потока вектора напряженности поверхность разбивается на небольшие участки, которые можно считать плоскими, а поле в пределах каждого из них однородным. Затем находят элементарные потоки вектора напряженности N _i через малые площадки S _i по формуле 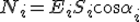. Полный поток через поверхность равен алгебраической сумме элементарных потоков через все ее участки:

)

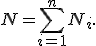Теорема Остроградского-Гаусса

Определим поток напряжённости поля электрических зарядов через некоторую замкнутую поверхность, окружающую эти заряды. Рассмотрим сначала случай сферической поверхности радиуса R, окружающей один заряд, находящийся в ее центре (рис. 13.6). 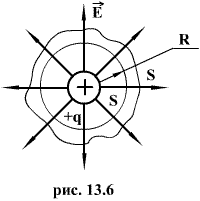Напряженность поля по всей сфере одинакова и равна

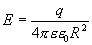
Силовые линии направлены по радиусам, т.е. перпендикулярны поверхности сферы 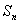, следовательно

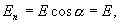
т.к.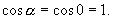
Тогда поток напряженности 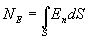будет равен

Используя формулу напряжённости, находим

Окружим теперь сферу произвольной замкнутой поверхностью S’. Каждая силовая линия, пронизывающая сферу, пронижет и эту поверхность. Следовательно формула (13.6) справедлива не только для сферы, но и для любой замкнутой поверхности. Если произвольной поверхностью окружаем n зарядов, то очевидно, что поток напряженности через эту поверхность равен сумме потоков, создаваемых каждым из зарядов, т.е.

Или

Таким образом, полный поток вектора напряженности электростатического поля через замкнутую поверхность произвольной формы численно равен алгебраической сумме свободных электрических зарядов, заключенных внутри этой поверхности, поделенной на . Это положение называется теоремой Остроградского - Гаусса. С помощью этой теоремы можно определить напряженность полей, создаваемых заряженными телами различной формы.

Поле равномерно заряженной бесконечной плоскости. Бесконечная плоскость (рис. 1) заряжена с постоянной поверхностной плотностью +σ (σ = dQ/dS — заряд, который приходится на единицу поверхности). Линии напряженности перпендикулярны данной плоскости и направлены от нее в каждую из сторон. Возьмем в качестве замкнутой поверхности цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности поля (соsα=0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания (площади оснований равны и для основания Е_n совпадает с Е), т. е. равен 2ES. Заряд, который заключен внутри построенной цилиндрической поверхности, равен σS. Согласно теореме Гаусса, 2ES=σS/ε₀, откуда

(1)

Из формулы (1) следует, что Е не зависит от длины цилиндра, т. е. напряженность поля на любых расстояниях равна по модулю, иными словами, поле равномерно заряженной плоскости однородно.

Поле двух бесконечных параллельных разноименно заряженных плоскостей (рис. 2). Пусть плоскости заряжены равномерно разными по знаку зарядами с поверхностными плотностями +σ и –σ. Поле таких плоскостей будем искать как суперпозицию полей, которые создаваются каждой из плоскостей в отдельности. На рисунке верхние стрелки соответствуют полю от положительно заряженной плоскости, нижние — от отрицательно заряженной плоскости. Слева и справа от плоскостей поля вычитаются (поскольку линии напряженности направлены навстречу друг другу), значит здесь напряженность поля E=0. В области между плоскостями E = E₊ + E_- (E₊ и E_- находятся по формуле (1)), поэтому результирующая напряженность

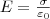(2)

Значит, результирующая напряженность поля в области между плоскостями описывается зависимостью (2), а вне объема, который ограничен плоскостями, равна нулю.

Дата добавления: 2015-04-24