Энергия взаимодействия двух равномерно заряженных параллельных пластин

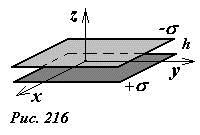
Найдем энергию взаимодействия двух равных по модулю зарядов противоположного знака, равномерно распределенными по двум параллельным пластинам. Обозначим поверхностную плотность заряда на одной пластине + σ, а на другой - σ. Расстояние между пластинами h будем считать значительно меньшим размеров пластин, площадь каждой пластины обозначим S. Краевыми эффектами пренебрежем.

Для расчета энергии взаимодействия воспользуемся формулой U = qφ’, где φ’ - потенциал поля создаваемого всеми зарядами, кроме заряда q.

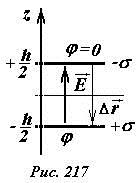
Напряженность поля между пластинами была вычислена нами ранее, она равна

. (5)

Для «упрощения» расчетов положим потенциал отрицательно заряженной пластины равным нулю, тогда потенциал другой пластины будет равен

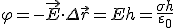. (6)

Здесь - вектор перемещения от отрицательной пластины к положительной. Данная формула определяет потенциал поля, создаваемого зарядами на обеих пластинах.

Теперь необходимо найти потенциал поля φ’, создаваемого только одной пластиной. Напряженность поля E’, создаваемого одной пластиной в два раза меньше напряженности поля между пластинами 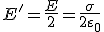, поэтому искомый потенциал будет равен 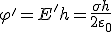. Таким образом, энергия взаимодействия зарядов оказывается равной

, (7)

здесь σS - заряд положительно заряженной пластины.

Не смотря на то, что противоположно заряженные пластины притягиваются, их энергия оказалась положительной – в этом нет ничего удивительного: мы положили потенциал одной из пластин равным нулю. Это значит, что нулевой энергии соответствует положение, когда положительно заряженная пластина совпадает с отрицательно заряженной, то есть когда пластины совпадают, а электрическое поле отсутствует. Если пластины находятся на некотором расстоянии h друг от друга, то при их сближении поле совершит положительную работу. Наоборот, чтобы разнести пластины, внешние силы должны совершить работу, увеличивая энергию системы.

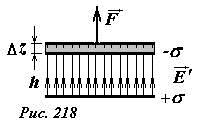
Энергию рассматриваемой системы можно найти, рассчитывая работу внешних сил, по разнесению пластин. На одну из пластин со стороны другой действует сила электрического притяжения 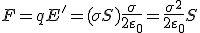, причем эта сила не зависит от расстояния между пластинами. Для того, чтобы раздвинуть пластины на расстояние h, необходимо приложить внешнюю силу, равную по модулю силе электрического притяжения (рис. 218). При этом эта сила совершит работу (равную увеличению энергии системы)

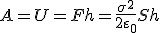. (7')

Таким образом, мы получаем ту же формулу для энергии систему зарядов. Используя соотношение между напряженностью поля между пластинами и поверхностной плотностью заряда σ = ε ₀ E, выразим энергию взаимодействия через напряженность поля

. (8)

В процессе разнесения пластин создается электрическое поле во все большем объеме между пластинами, поэтому можно утверждать, что совершенная работа увеличивает энергию электрического поля, или работа расходуется на создание поля. Так при смещении пластины на расстояние Δ z, объем занятый полем увеличивается на S Δ z, если расстояние между пластинами увеличилось от нуля до некоторого значения h, то поле создается в объеме Sh. Таким образом, найденная энергия взаимодействия зарядов (7) есть энергия электрического поля - энергия «размазанная» по той области пространства, где создано поле. Косвенным подтверждением сделанного заключения, является тот факт, что энергия взаимодействия пропорциональна объему части пространства V = Sh, занятого полем и выражается через характеристику поля (его напряженность) – в формуле (8) нет характеристик зарядов. Электрическое поле, уже благодаря своему существованию обладает энергией. В качестве энергетической характеристики поля следует рассматривать энергию, содержащуюся в единице объема, то есть объемную плотность энергии: 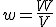. Из выражения (8) следует, что объемная плотность энергии электрического поля определяется формулой

. (9)

Как обычно, в неоднородном поле корректное определение плотности энергии «в данной точке» требует предельного перехода: плотностью энергии электрического поля называется отношение энергии поля, заключенной в малом объеме к величине этого объема, при стремлении последнего к нулю

, при Δ V → 0.

Дата добавления: 2015-04-24