Носители тока в металлах. Опыты Толмена и Стюарта. Природа электрического сопротивления. Сверхпроводимость

Для выяснения природы носителей тока в металлах был поставлен ряд опытов.

Опыт Рикке (Riecke C., 1845-1915). В 1901г. Рикке осуществил опыт, в котором он пропускал ток через стопку цилиндров с тщательно отполированными торцами Cu-Al-Cu (рис.6.1). Перед началом опыта образцы были взвешены с высокой степенью точности (Δm = ±0,03 мг). Ток пропускался в течение года. За это время через цилиндры прошел заряд q = 3,5∙106Кл.

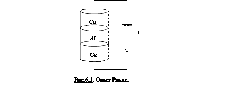
По окончании опыта цилиндры были вновь взвешены. Взвешивание показало, что пропускание тока не оказало никакого влияния на вес цилиндров. При исследовании торцевых поверхностей под микроскопом также не было обнаружено проникновения одного металла в другой. Результаты опыта Рикке свидетельствовали о том, что носителями тока в металлах являются не атомы, а какие-то частицы, которые входят в состав всех металлов.

Такими частицами могли быть электроны, открытые в 1897г. Томсоном (Thomson J., 1856-1940) в опытах с катодными лучами. Чтобы отождествить носители тока в металлах с электронами, необходимо было определить знак и величину удельного заряда носителей. Это было осуществлено в опыте Толмена и Стюарта (Tolman R., 1881-1948, Stewart B., 1828-1887).

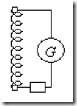
Опыт Толмена и Стюарта. Суть опыта, проведенного в 1916г., состояла в определении удельного заряда носителей тока при резком торможении проводника (рис.6.2). В опыте для этой цели использовалась катушка из медного провода длиной 500м, которая приводилась в быстрое вращение (линейная скорость витков составляла 300м/с), а затем резко останавливалась. Заряд, протекавший по цепи за время торможения, измерялся с помощью баллистического гальванометра.

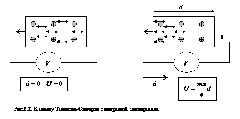
Найденный из опыта удельный заряд носителя тока 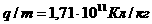, оказался очень близким к величине удельного заряда электрона 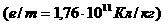, откуда был сделан вывод о том, что ток в металлах переносится электронами.

Физическая природа электрического сопротивления. При движении свободных электронов в проводнике они сталкиваются на своем пути с положительными ионами 2 (см. рис. 10, а), атомами и молекулами вещества, из которого выполнен проводник, и передают им часть своей энергии. При этом энергия движущихся электронов в результате столкновения их с атомами и молекулами частично выделяется и рассеивается в виде тепла, нагревающего проводник. Ввиду того что электроны, сталкиваясь с частицами проводника, преодолевают некоторое сопротивление движению, принято говорить, что проводники обладают электрическим сопротивлением. Если сопротивление проводника мало, он сравнительно слабо нагревается током; если сопротивление велико, проводник может раскалиться. Провода, подводящие электрический ток к электрической плитке, почти не нагреваются, так как их сопротивление мало, а спираль плитки, обладающая большим сопротивлением, раскаляется докрасна. Еще сильнее нагревается нить электрической лампы.
За единицу сопротивления принят ом. Сопротивлением 1 Ом обладает проводник, по которому проходит ток 1 А при разности потенциалов на его концах (напряжении), равной 1 В. Эталоном сопротивления 1 Ом служит столбик ртути длиной 106,3 см и площадью поперечного сечения 1 мм2 при температуре 0°С. На практике часто сопротивления измеряют тысячами ом — килоомами(кОм) или миллионами ом — мегаомами (МОм). Сопротивление обозначают буквой R (r).
Проводимость. Всякий проводник можно характеризовать не только его сопротивлением, но и так называемой проводимостью — способностью проводить электрический ток. Проводимость есть величина, обратная сопротивлению. Единица проводимости называется сименсом (См). 1 См равен 1/1 Ом. Проводимость обозначают буквой G (g). Следовательно,

G = 1 / R (4)

Удельное электрическое сопротивление и проводимость. Атомы разных веществ оказывают прохождению электрического тока неодинаковое сопротивление. О способности отдельных веществ проводить электрический ток можно судить по их удельному электрическому сопротивлению р. За величину, характеризующую удельное сопротивление, обычно принимают сопротивление куба с ребром 1 м. Удельное электрическое сопротивление измеряют в Ом*м. Для суждения об электропроводности материалов пользуются также понятием удельная электрическая проводимость?=1/?. Удельная электрическая проводимость измеряется в сименсах на метр (См/м) (проводимость куба с ребром 1м). Часто удельное электрическое сопротивление выражают в ом-сантиметрах (Ом*см), а удельную электрическую проводимость — в сименсах на сантиметр (См/см). При этом 1 Ом*см = 10-2Ом*м, а 1 См/см = 102См/м.

Проводниковые материалы применяют, главным образом, в виде проволок, шин или лент, площадь поперечного сечения которых принято выражать в квадратных миллиметрах, а длину — в метрах. Поэтому для удельного электрического сопротивления подобных ма­териалов и удельной электрической проводимости введены и другие единицы измерения:? измеряют в Ом*мм2/м (сопротивление про­водника длиной 1 м и площадью поперечного сечения 1 мм2), а? — в См*м/мм2(проводимость проводника длиной 1 м и пло­щадью поперечного сечения 1 мм2).

Из металлов наиболее высокой электропроводностью обладают серебро и медь, так как структура их атомов позволяет легко пере­двигаться свободным электронам, затем следует золото, хром, алю­миний, марганец, вольфрам и т. д. Хуже проводят ток железо и сталь.

Чистые металлы всегда проводят электрический ток лучше, чем их сплавы. Поэтому в электротехнике используют преимущественно очень чистую медь, содержащую только 0,05 % примесей. И наобо­рот, в тех случаях, когда необходим материал с высоким сопротив­лением (для различных нагревательных приборов, реостатов и пр.), применяют специальные сплавы: константан, манганин, нихром, фех­раль.

Следует отметить, что в технике, кроме металлических проводников, используют и неметаллические. К таким проводникам относится, например, уголь, из которого изготовляют щетки электрических машин, электроды для прожекторов и пр. Проводниками электрического тока являются толща земли, живые ткани растений, животных и человека. Проводят электрический ток сырое дерево и многие другие изоляционные материалы во влажном состоянии.
Электрическое сопротивление проводника зависит не только от материала проводника, но и его длины l и площади поперечного сечения s. (Электрическое сопротивление подобно сопротивлению, оказываемому движению воды в трубе, которое зависит от площади сечения трубы и ее длины.)
Сопротивление прямолинейного проводника

R =?l / s (5)

Если удельное сопротивление? выражено в Ом*мм /м, то для того чтобы получить сопротивление проводника в омах, длину его надо подставлять в формулу (5) в метрах, а площадь поперечного сечения — в квадратных миллиметрах.

Зависимость сопротивления от температуры. Электропроводность всех материалов зависит от их температуры. В металлических проводниках при нагревании размах и скорость колебаний атомов в кристаллической решетке металла увеличиваются, вследствие чего возрастает и сопротивление, которое они оказывают потоку электро­нов. При охлаждении происходит обратное явление: беспорядоч­ное колебательное движение атомов в узлах кристаллической решетки уменьшается, сопротивление их потоку электронов пони­жается и электропроводность проводника возрастает.

В природе, однако, имеются некоторые сплавы: фехраль, константан, манганин и др., у которых в определенном интервале температур электрическое сопротивление меняется сравнительно мало. Подобные сплавы применяют в технике для изготовления различных резисторов, используемых в электроизмерительных при­борах и некоторых аппаратах для компенсации влияния темпера­туры на их работу.

О степени изменения сопротивления проводников при измене­нии температуры судят по так называемому температурному ко­эффициенту сопротивления а. Этот коэффициент представляет собой относительное приращение сопротивления проводника при увеличении его температуры на 1 °С. В табл. 1 приведены значения температурного коэффициента сопротивления для наиболее приме­няемых проводниковых материалов.

Сопротивление металлического проводника Rtпри любой тем­пературе t

Rt= R0[ 1 +? (t - t0) ] (6)

где R0— сопротивление проводника при некоторой начальной темпера­туре t0(обычно при + 20 °С), которое может быть подсчитано по формуле (5);

t— t0— изменение температуры.

Свойство металлических проводников увеличивать свое сопро­тивление при нагревании часто используют в современной технике для измерения температуры. Например, при испытаниях тяговых двигателей после ремонта температуру нагрева их обмоток опре­деляют измерением их сопротивления в холодном состоянии и после работы под нагрузкой в течение установленного периода (обычно в течение 1 ч).

Исследуя свойства металлов при глубоком (очень сильном) охлаждении, ученые обнаружили замечательное явление: вблизи абсолютного нуля (— 273,16 °С) некоторые металлы почти пол­ностью утрачивают электрическое сопротивление. Они становятся идеальными проводниками, способными длительное время пропус­кать ток по замкнутой цепи без всякого воздействия источника электрической энергии. Это явление названо сверхпроводимостью. В настоящее время созданы опытные образцы линий электропере­дачи и электрических машин, в которых используется явление сверхпроводимости. Такие машины имеют значительно меньшие мас­су и габаритные размеры по сравнению с машинами общего назна­чения и работают с очень высоким коэффициентом полезного дей­ствия. Линии электропередачи в этом случае можно выполнить из проводов с очень малой площадью поперечного сечения. В пер­спективе в электротехнике будет все больше и больше использо­ваться это явление.

Сверхпроводи́мость — свойство некоторых материалов обладать строго нулевым электрическим сопротивлением при достижении ими температуры ниже определённого значения (критическая температура). Известны несколько десятков чистых элементов, сплавов и керамик , переходящих в сверхпроводящее состояние. Сверхпроводимость — квантовое явление . Оно характеризуется также эффектом Мейснера , заключающемся в полном вытеснении магнитного поля из объема сверхпроводника. Существование этого эффекта показывает, что сверхпроводимость не может быть описана просто как идеальная проводимость в классическом понимании.

Открытие в 1986—1993 гг. ряда высокотемпературных сверхпроводников (ВТСП) далеко отодвинуло температурную границу сверхпроводимости и позволило практически использовать сверхпроводящие материалы не только при температуре жидкого гелия (4.2 К), но и при температуре кипения жидкого азота (77 К), гораздо более дешевой криогенной жидкости.

13. собственная проводимость полупроводников. Примесная проводимость полупроводников. Электрический ток через р-п переход. Вольтамперная характеристика диода.

СОБСТВЕННАЯ ПРОВОДИМОСТЬ - проводимость полупроводника , обусловленная электронами, возбуждёнными из валентной зоны в зону проводимости и дырками, образовавшимися в валентной зоне. Концентрации ni таких (зонных) электронов н дырок равны, и их можно выразить через эфф. плотности состояний в зоне проводимости (Nc)и в валентной зоне (Nv), ширину запрещённой зоны и абс. темп-ру Т:

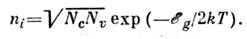
Т. к. проводимость 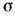полупроводника пропорциональна концентрации свободных носителей заряда и их подвижности 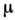, то в пренебрежении слабыми степенными зависимостями Nc, Nv и 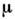от темп-ры для собств. полупроводников можно получить соотношение:

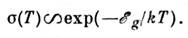
При наличии примесей, обусловливающих примесную проводимость полупроводника, С. п. можно наблюдать в диапазоне изменения темп-ры полупроводника, в к-ром зависимость 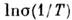линейна. Лит. см. при ст. Полупроводники. И. Л. Бейиихес.

Проводимость полупроводников, обусловленная примесями, называется примесной проводимостью, а сами полупроводники — примесными полупроводниками. Примесная проводимость обусловлена примесями (атомы посторонних элементов), а также дефек­тами типа избыточных атомов (по сравнению со стехиометрическим составом), тепло­выми (пустые узлы или атомы в междоузлиях) и механическими (трещины, дислокации и т. д.) дефектами. Наличие в полупроводнике примеси существенно изменяет его проводимость. Например, при введении в кремний примерно 0,001 ат.% бора его проводимость увеличивается примерно в 106раз.

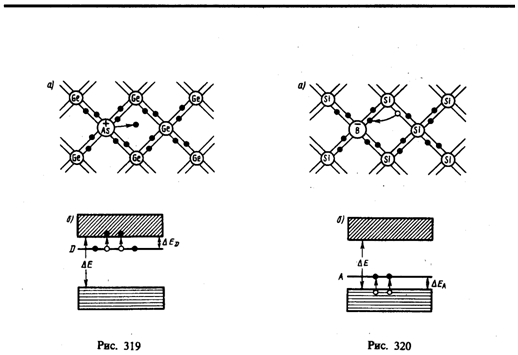
Примесную проводимость полупроводников рассмотрим на примере Ge и Si, в которые вводятся атомы с валентностью, отличной от валентности основных атомов на единицу. Например, при замещении атома германия пятивалентным атомом мышьяка (рис. 319, а) один электрон не может образовать ковалентной связи, он оказыва­ется лишним и может быть легко при тепловых колебаниях решетки отщеплен от атома, т. е. стать свободным. Образование свободного электрона не сопровождается нарушением ковалентной связи; следовательно дырка не возникает. Избыточный положительный заряд, возникающий вблизи атома примеси, связан с атомом примеси и поэтому перемещаться по решетке не может.

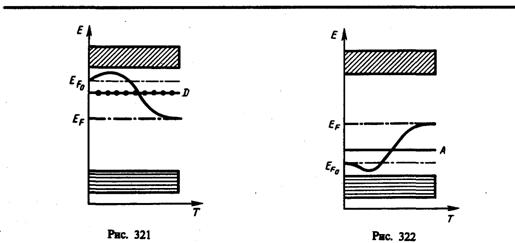
С точки зрения зонной теории рассмотренный процесс можно представить следу­ющим образом (рис. 319, б). Введение примеси искажает поле решетки, что приводит к возникновению в запрещенной зоне энергетического уровня D валентных электронов мышьяка, называемого примесным уровнем. В случае германия с примесью мышьяка этот уровень располагается от дна зоны проводимости на расстоянии D ED =0,013 эВ. Так как D ED < kT, то уже при обычных температурах энергия теплового движения достаточна для того, чтобы перебросить электроны примесного уровня в зону проводимости; образующиеся при этом положительные заряды локализуются на неподвижных атомах мышьяка и в проводимости не участвуют.

Таким образом, в полупроводниках с примесью, валентность которой на единицу больше валентности основных атомов, носителями тока являются электроны; воз­никает электронная примесная проводимость (проводимость n -типа). Полупроводники с такой проводимостью называются электронными (или полупроводниками n -типа). Примеси, являющиеся источником электронов, называются донорами, а энергетические уровни этих примесей — донорными уровнями.

Предположим, что в решетку кремния введен примесный атом с тремя валентными электронами, например бор (рис. 320, а). Для образования связей с четырьмя ближай­шими соседями у атома бора не хватает одного электрона, одна из связей остается неукомплектованной и четвертый электрон может быть захвачен от соседнего атома основного вещества, где соответственно образуется дырка. Последовательное заполнение образующихся дырок электронами эквивалентно движению дырок в полупроводнике, т. е. дырки не остаются локализованными, а перемещаются в решетке кремния как свободные положительные заряды. Избыточный же отрицательный заряд, воз­никающий вблизи атома примеси, связан с атомом примеси и по решетке перемещаться не может.

По зонной теории, введение трехвалентной примеси в решетку кремния приводит к возникновению в запрещенной зоне примесного энергетического уровня А, не занято­го электронами. В случае кремния с примесью бора этот уровень располагается выше верхнего края валентной зоны на расстоянии D EA =0,08 эВ (рис. 320, б). Близость этих уровней к валентной зоне приводит к тому, что уже при сравнительно низких температурах электроны из валентной зоны переходят на примесные уровни и, связываясь с атомами бора, теряют способность перемещаться по решетке кремния, т. е. в проводимости не участвуют. Носителями тока являются лишь дырки, возникающие в валентной зоне.

Таким образом, в полупроводниках с примесью, валентность которой на единицу меньше валентности основных атомов, носителями тока являются дырки; возникает дырочная проводимость (проворность p -типа). Полупроводники с такой проводимостью называются дырочными (или полупроводниками p -типа). Примеси, захватывающие электроны из валентной зоны полупроводника, называются акцепторами, а энергетические уровни этих примесей — акцепторными уровнями.

В отличие от собственной проводимости, осуществляющейся одновременно элект­ронами и дырками, примесная проводимость полупроводников обусловлена в основ­ном носителями одного знака: электронами — в случае донорной примеси, дырка­ми — в случае акцепторной. Эти носители тока называются основными. Кроме основ­ных носителей в полупроводнике имеются и неосновные носители: в полупроводниках n -типа — дырки, в полупроводниках p- типа — электроны.

Наличие примесных уровней в полупроводниках существенно изменяет положение уровня Ферми ЕF. Расчеты показывают, что в случае полупроводников n -типа уровень Ферми ЕF0 при 0 К расположен посередине между дном зоны проводимости и донорным уровнем (рис. 321), С повышением температуры все большее число электронов переходит из донорных состояний в зону проводимости, но, помимо этого, возрастает и число тепловых флуктуаций, способных возбуждать электроны из валентной зоны и перебрасывать их через запрещенную зону энергий. Поэтому при высоких температурах уровень Ферми имеет тенденцию смещаться вниз (сплошная кривая) к своему предельному положению в центре запрещенной зоны, характерному для собственного полупроводника.

Уровень Ферми в полупроводниках р- типа при 0 К ЕF0 располагается посередине между потолком валентной зоны и акцепторным уровнем (рис. 322). Сплошная кривая опять-таки показывает его смещение с температурой. При температурах, при которых примесные атомы оказываются полностью истощенными и увеличение концентрации носителей происходит за счет возбуждения собственных носителей, уровень Ферми располагается посередине запрещенной зоны, как в собственном полупроводнике.

Проводимость примесного полупроводника, как и проводимость любого провод­ника, определяется концентрацией носителей и их подвижностью. С изменением тем­пературы подвижность носителей меняется по сравнительно слабому степенному зако­ну, а концентрация носителей — по очень сильному экспоненциальному закону, поэто­му проводимость примесных полупроводников от температуры определяется в основ­ном температурной зависимостью концентрации носителей тока в нем. На рис. 323 дан примерный график зависимости ln g от 1/ T для примесных полупроводников. Участок AB описывает примесную проводимость полупроводника. Рост примесной проводимо­сти полупроводника с повышением температуры обусловлен в основном ростом концентрации примесных носителей. Участок ВС соответствует области истощения примесей (это подтверждают и эксперименты), участок CD описывает собственную проводимость полупроводника.

СТРУКТУРА И ОСНОВНЫЕ СВОЙСТВА р-n ПЕРЕХОДА

Прежде всего, рассмотрим два образца полупроводника с электронной и дырочной электропроводностями (рис. 1.6, а). Напомним, что в дырочном полупроводнике присутствуют в равном количестве подвижные положительные дырки и неподвижные отрицательные ионы. На рис. 1.6,а дырки обозначены знаками «плюс», а отрицательные ионы - знаками «минус», заключенными в кружки. Для нашего рисунка концентрация примеси в электронном полупроводнике выбрана в 2 раза меньше, чем в дырочном. Аналогично обозначениям зарядов в дырочном полупроводнике в электронном полупроводнике электроны обозначены знаками «минус», а положительные ионы - со знаками «плюс», заключенными в кружки. Поскольку N A = 2 N Д, то заряды в дырочном полупроводнике нарисованы в 2 раза чаще, чем в электронном.

Теперь представим, что рассмотренные нами два образца являются просто областями единого кристалла полупроводника (рис. 1.6, б). Тогда по закону диффузии электроны из области n будут перемещаться в область р, а дырки, наоборот, - из области р в область n. Встречаясь на границе р и п областей, дырки и электроны рекомбинируют. Следовательно, в этой пограничной области значительно уменьшается концентрация носителей заряда и обнажаются некомпенсированные заряды неподвижных ионов. Со стороны области обнажаются положительные заряды доноров, а со стороны области р -отрицательные заряды акцепторов. Область некомпенсированных неподвижных зарядов и есть собственно область р-п перехода. Ее часто называют обедненным, истощенным слоем, или i -областью, имея ввиду резко сниженную концентрацию подвижных носителей заряда. Иногда эту область называют запорным слоем электронно-дырочного перехода.

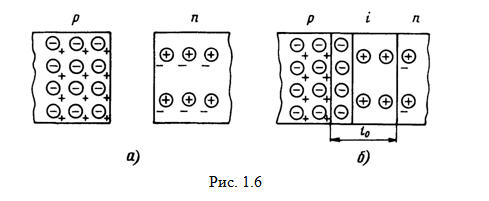
Отметим, что р-п переход в целом должен быть электронейтральным, т.е. отрицательный заряд левой части и положительный заряд правой части должны быть одинаковы. Поскольку в рассматриваемом нами случае N A = 2 N Д(несимметричный переход), протяженность областей расположения заряд оказывается разной: одну треть i -области занимают акцепторы, а две трети доноры. Таким образом, большая часть обедненной области сосредоточивается в слаболегированном (высокоумном) слое.

В реальных р-п переходах концентрации доноров и акцепторов отличаются на несколько порядков. В таких несимметричных переходах практически весь обедненный слой сосредоточен в слаболегированной части. Ширина обедненного слоя (i -области) в равновесном состоянии l 0 (см. рис. 1.6, б) является важным параметром р-п перехода. Другим, не менее важным параметром равновесного состояния является высота потенциального барьера (контактная разность потенциалов) ∆φ0. Этот параметр показан на зонной энергетической диаграмме р-п перехода, изображенной на рис. 1.7 (где εF- уровень Ферми).

Потенциальный барьер образуется электрическим полем пространственного заряда обедненного слоя. При отсутствии внешнего поля (равновесное состояние) уровень Ферми является общим для всего объема полупроводника и расположен в запрещенной зоне. Поскольку в полупроводнике п -типа уровень Ферми смещен вверх относительно середины запрещенной зоны, а в полупроводнике р -типа вниз, то разрешенные зоны дырочной области должны располагаться на более высоких энергиях, чем разрешенные зоны электронной энергии. Следовательно, в обедненном слое диаграмма энергетических зон искривляется. Заметим, что в i -области уровень Ферми проходит вблизи середины запрещенной зоны.

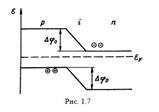
Электрическое поле электронно-дырочного перехода, представляемое на рис. 1.7 потенциальным барьером, препятствует прохождению электронов из области р -типа в область п -типа и дырок в обратном направлении. Более строго: дрейфовые составляющие тока равны диффузионным. С некоторым приближением можно считать, что в равновесном состоянии р-п перехода его внутреннее электрическое поле компенсирует процесс диффузии носителей заряда, в результате чего ток через р-п переход не протекает. Анализируя рис. 1.7, следует помнить, что электроны в зоне проводимости стремятся занять уровни минимальной энергии, а дырки в валентной зоне - максимальной энергии.

Высоту потенциального барьера ∆φ0удобно выражать в единицах напряже­ния - вольтах. Довольно сильное влияние на величину ∆φ0оказывает шири­на запрещенной зоны исходного полупроводника: чем больше εз, тем больше и ∆φ0. Так, для большинства р-п переходов из германия ∆φ0= 0,35 В. а из кремния - 0,7 В.

Ширина р-п перехода во многом определяется величиной ∆φ0. Это хорошо видно из общей формулы для l0 при N a›› N д:

(1.5)

где εo, εn- диэлектрическая проницаемость вакуума и полупроводника соот­ветственно. Величина l 0обычно составляет десятые доли или единицы микро­метра. Из (1.5) следует, что для создания широкого р-п перехода следует ис­пользовать малые концентрации примеси, а для создания узкого перехода - большие концентрации. При равных концентрациях примеси l 0будет больше у р-п перехода с большим ∆φ0и, следовательно, с большей εз. Таким образом, у кремниевых р-п переходов l 0обычно больше, чем у германиевых.

Если к р-п переходу подключить внешний источник напряжения, то нару­шится условие равновесия и потечет ток. При этом должна измениться высота потенциального барьера и соответственно ширина р-п перехода.

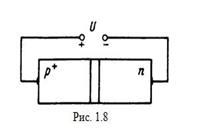
Рассмотрим сначала прямое смещение р-п перехода (рис. 1,8). В этом случае внешнее напряжение U приложено в прямом направлении, т. е. знаком «плюс» к области р- типа. Высота потенциального барьера ∆φ при этом снижается: ∆φ = ∆φ0- U

Заменив в (1.5) ∆φ0на ∆φ и подставив в (1.5), можно убедиться, что и ширина р-п перехода уменьшается при прямом смещении.

Уменьшение высоты потенциального барьера приводит к снижению элек­трического поля, препятствующего диффузии носителей заряда. Дырки из области р- типа начинают переходить в область n -типа, а электроны, наоборот, из области р- типа в область n -типа. В каждой области появляются избыточные концентрации неосновных носителей. Процесс нагнетания неосновных носите­лей заряда в какую-либо область полупроводника называется инжекцией.

За счет разной концентрации примеси в областях несимметричных р-п переходов концентрации основных носителей тоже будут разные (обычно отличаются на несколько порядков). В рассматриваемом нами случае N a›› N д, следовательно, рр» рп. Сильнолегированную дырочную область обозначим как р+ (рис. 1.8). Она имеет относительно малое удельное сопротивление и обычно называется эмиттером. Область n -типа, имеющая относительно большое удельное сопротивление, называется базой.

В несимметричных р-п переходах концентрация инжектированных носите­лей из эмиттера в базу всегда гораздо больше, чем в обратном направлении. Параметром, характеризующим степень однонаправленности инжекции, яв­ляется коэффициент инжекции γ. Для рассматриваемого нами перехода можно записать

γ = I р / ( I р+ I n),

где Ip, In - токи инжекции дырок и электронов соответственно. В реальных р-п переходах инжекция имеет практически односторонний характер: носители инжектируются в основном из эмиттера в базу (I р›› I n), т. е. γ ≈ 1. Для практиче­ских расчетов удобно использовать формулу

γ = 1 — ρэ/ρб

где ρэ, ρб- удельные сопротивления эмиттера и базы соответственно. Из (1.7) следует, что чем сильнее легирован эмиттер и чем слабее легирована база, тем ближе значение у к единице.

Теперь рассмотрим обратное смещение р-п перехода (рис. 1.9). В этом случае внешнее напряжение U приложено в обратном направлении, т. е. знаком «плюс» к области n-типа. Высота потенциального барьера ∆φ при этом повышается: ∆φ = ∆φ0+ U

Подставляя значение ∆φ из (1.8) в формулу (1.5), получаем для неравновес­ной ширины р-п перехода l: 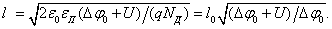Таким образом, увеличение обратного смещения приводит к расширению р-п перехода. Поскольку несимметричный переход почти полностью расположен в высокоомной базе, то и его расширение происходит в сторону базы. При использовании обратного смещения р-п перехода на практике обычно U» ∆φ. В этом случае (1.9) можно переписать в виде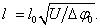

При приложении U в обратном направлении концентрации неосновных носителей на границах i -области уменьшаются по сравнению с равновесными значениями. Такой процесс отсоса носителей называется экстракцией.

Вольт-амперная характеристика (ВАХ) — график зависимости тока через двухполюсник от напряжения на этом двухполюснике. Вольт-амперная характеристика описывает поведение двухполюсника на постоянном токе . Чаще всего рассматривают ВАХ нелинейных элементов (степень нелинейности определяется коэффициентом нелинейности 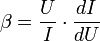), поскольку для линейных элементов ВАХ представляет собой прямую линию и не представляет особого интереса.

Характерные примеры элементов, обладающих существенно нелинейной ВАХ: диод, динистор, стабилитрон.

Для трехполюсных элементов (таких, как транзистор, тиристор или ламповый триод) часто строят семейства кривых, являющимися ВАХ для двухполюсника при так или иначе заданных параметрах на третьем выводе элемента.

Необходимо отметить, что в реальной схеме, особенно работающей с относительно высокими частотами (близкими к границам рабочего частотного диапазона) для данного устройства реальная зависимость напряжения от времени может пробегать по траекториям, весьма далеким от «идеальной» ВАХ. Чаще всего это связано с емкостью или другими инертными свойствами элемента.

14.

Дата добавления: 2015-04-24