Закон Ома для замкнутой цепи. Сторонние силы. Электродвижущая сила элемента

Классическая теория электропроводности металлов. Закон Ома для проводника в дифференциальной и интегральной форме.

Изучив основные законы постоянного тока, познакомимся с тем, как их объясняет классическая теория в случае металлических проводников.

1) Прежде всего, согласимся с тем, что свободными носителями заряда в металлах являются не ионы, а электроны.

2) По теории Друде-Лоренца, свободные электроны в металле движутся также как атомы идеального газа. Эта аналогия позволила вычислить среднюю скорость теплового движения электронов. Для температуры Т = 300 К она составила гигантскую величину: 10⁵ м/с 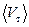» 10⁵ м/с.

3) Теперь обратимся к рассмотрению направленного движения электронов в электрическом поле. Электрон движется равноускоренно под действием постоянной силы F = eE. Ускорение движения (II закон Ньютона): За время свободного пробега 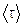электрон достигнет максимальной скорости в своём направленном движении: .

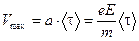после каждого столкновения скорость направленного движения вновь начинает нарастать от 0 до V _max. Тогда средняя скорость направленного движения оказывается равной половине максимальной:

. Воспользовавшись этим результатом в уравнении (6.2), получим: .

Коэффициент пропорциональности, связывающий плотность тока с напряженностью электростатического поля - удельная электропроводность металла:

4) К концу своего свободного пробега электрон достигает скорости: 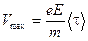и энергии: .

называется законом Ома в интегральной форме.

Уравнение 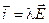. — математическая запись закона Ома в дифференциальной форме.

Нельзя организовать циркуляцию заряда по замкнутому контуру под действием только электростатической силы. Для переноса заряда в область высокого потенциала (2- b -1) придётся использовать силы неэлектростатической природы. Такие силы получили название сторонних сил. В качестве сторонних сил могут выступать любые силы кроме электростатических. Приборы, в которых на электрические заряды действуют сторонние силы, называются источниками тока. В аккумуляторах, например, сторонние силы возникают в результате химической реакции взаимодействия электродов с электролитом, в генераторах сторонними являются силы, действующие на заряды, движущиеся в магнитном поле и т.д. Именно в источниках тока благодаря работе сторонних сил создаётся генерируемая энергия, которая затем расходуется в электрической цепи.

Работа, которую совершают сторонние силы 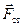при перемещении единичного положительного заряда — одна из основных характеристик источника, его электродвижущая сила e:

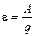
Поле сторонних сил, также как и электростатическое поле, характеризуется вектором напряжённости :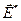

Электродвижущая сила источника равна работе, совершаемой сторонними силами при перемещении единичного положительного заряда по замкнутому контуру.

На участке цепи 1-а-2 движение носителей заряда происходит под действием только электростатической силы 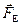= q . Такие участки называются однородными.

Участок замкнутого контура, где наряду с электростатической силой действуют и сторонние силы, называют неоднородным.

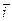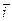Можно показать, что на однородном участке цепи средняя скорость направленного движения носителей заряда пропорциональна действующей на них силе. Для этого достаточно сравнить формулы, полученные на прошлой лекции: = (6.3) и = l

Пропорциональность скорости силе, а плотности тока — напряжённости сохранится и в случае неоднородного участка цепи. Но теперь напряжённость поля равна сумме напряжённостей электростатического поля и поля сторонних сил : .

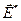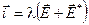Это уравнение закона Ома в локальной дифференциальной форме для неоднородного участка цепи.

Теперь перейдём к закону Ома для неоднородного участка цепи в интегральной форме.

Для замкнутого контура уравнение закона Ома несколько видоизменяется, так как разность потенциалов в этом случае равна нулю: .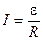

В законе Ома для замкнутой цепи (7.8) R — полное сопротивление контура, складывающееся из внешнего сопротивления цепи R₀ и внутреннего сопротивления источника r: R = R₀ + r.

12) Закон Джоуля-Ленца в дифференциальной форме и интегральной форме.

Пусть на участке электрической цепи протекает постоянный ток I. Напряжение U на концах этого участка численно равно работе, совершаемой электрическими силами при перемещении единичного положительного заряда по этому участку. Это следует из определения напряжения.

Отсюда работа A = q  ×  U. За время t по участку будет перенесён заряд q = I  ×  t и при этом будет совершена работа: A = q  ×  U = U  ×  I  ×  t.

Это выражение работы электрического тока справедливо для любых проводников.

Работа, совершаемая в единицу времени — мощность электрического тока: .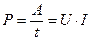

Работа электрического тока (6.14) может затрачиваться на нагревание проводника, совершение механической работы (электродвигатель) и на химическое действие тока при его течении через электролит (электролиз).

Если химическое действие и механическая работа при течении тока не производятся, то вся работа электрического тока расходуется только на нагревание проводника: Q = A = U  ×  I  ×  t = I ² ×  R  ×  t. (6.15)

Закон о тепловом эффекте электрического тока (6.15) был экспериментально установлен независимо английским учёным Д. Джоулем и русским академиком Э.Х. Ленцем. Формула (6.15) — математическая запись закона Джоуля-Ленца в интегральной форме, позволяющая вычислить количество теплоты, выделяющейся в проводнике.

.

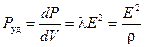Перед нами закон Джоуля-Ленца в дифференциальной форме.

Учитывая, что i = l E = 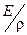, это выражение можно записать ещё и так:

Дата добавления: 2015-04-24