Агрегатных и индивидуальных индексов

Агрегатный индекс связан с индивидуальными индексами. При этом агрегатный индекс является некоторой средней из индивидуальных индексов с соответствующими весами.

Предположим, что известны индивидуальные индексы цен .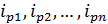

Тогда

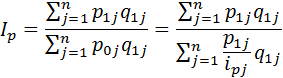
Данная формула представляет собой средневзвешенное гармоническое из индивидуальных индексов цен с весами .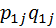

Предположим, что известны индивидуальные индексы физического объема .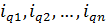

Тогда

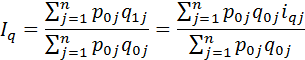
Данная формула представляет собой средневзвешенное арифметическое из индивидуальных индексов физических объемов с весами .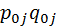

2. Сплошное и выборочное наблюдение. Понятие генеральной совокупности и выборки

Научно организованный сбор сведений, заключающийся в регистрации тех или иных признаков, относящихся к каждой единице (элементу) изучаемой совокупности, именуют статистическим наблюдением.

Статистическое наблюдение может быть сплошным и не сплошным. Сплошное наблюдение предполагает полный учет всех элементов изучаемой совокупности (например, перепись населения). К не сплошному наблюдению прибегают в тех случаях, когда физически невозможно или трудно осуществить сплошное наблюдение.

Не сплошное наблюдение может быть осуществлено по разному. Различают следующие его виды:

- наблюдение основного массива;

- выборочное наблюдение;

- монографическое наблюдение.

Наблюдение основного массива предполагает исключение из состава совокупности малозначимых единиц и исследование основной ее части.

При использовании наблюдения основного массива исходят из соображения, что исключение определенной части малозначимых единиц не отразится существенно на результатах, в то время как включение этих единиц значительно увеличит объем работы и соответственно затраты.

Из сказанного очевидно, что применение наблюдения основного массива возможно лишь в случаях, когда можно заранее решить какие единицы малозначимые, а какие нет.

При выборочном наблюдении характеристика всей совокупности дается по результатам исследования некоторой ее части (выборки), отобранной в случайном порядке (например, опросы перед выборами). Сама же изучаемая совокупность (множество всех элементов) называется генеральной совокупностью.

4. Суть группировки. Рекомендации по выбору числа групп. Расчет величины интервалов и определение их границ

В статистической практике этот этап статистического исследования называют группировкой.

Группировка представляет собой разбиение совокупности на группы, однородные по какому-либо признаку. Группировка основывается на группировочном признаке и интервале, который представляет собой промежуток между минимальным и максимальным значением признака в группе.

Интервалы могут быть равными и неравными, открытыми и закрытыми. Под закрытым интервалом понимают интервал, имеющий как нижнюю, так и верхнюю границу, например (100;200)). Под открытым интервалом понимают интервал, одна из границ которого равна 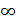(например, свыше 500).

При определении числа групп и величины интервалов следует иметь в виду, что число объектов в выделенных группах должно быть достаточным, чтобы характеристики, рассчитанные для отдельных групп, были статистически достоверными.

Существуют рекомендации по выбору числа групп k:

Число наблюдений (n)	Число групп (k)
25−40	5−6
40−60	6−8
60−200	8−12
> 200	10−15

Число групп также можно определить по формуле

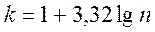
Наличие равных интервалов облегчает вычисление различных статистических характеристик.

Величина интервала вычисляется по формуле

,

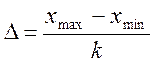где x _max − максимальное значение признака в исследуемой

совокупности;

x _min − минимальное значение признака в исследуемой

совокупности.

Затем определяются границы каждого интервала:

для первого интервала: от x _min до x _min +;

для второго интервала: от x _min+ до x _min +2;

………….

для k -го интервала: от x _min+(k -1) до x _max.

6. Аналитическая группировка. Признак-фактор и признак-результат

Аналитическая группировка служит для выявления зависимости между признаками. При этом выделяют признак-фактор и признак-результат. Группировка осуществляется по признаку-фактору. В каждой группе рассчитывается среднее значение признака-результата. Анализируя изменение средних значений признака-результата от группы к группе, можно сделать вывод о наличии или отсутствии взаимосвязи между признаками.

Различие групповых средних позволяет утверждать, что признаки взаимозависимы. Если изменение величины признака-фактора в определенном направлении вызывает изменение признака-результата в том же направлении, то говорят, что связь положительная, а в противном случае − отрицательная. Результаты аналитической группировки представляются в виде таблицы

Значение признака-фактора	Количество элементов совокупности в отдельной группе	Среднее значение признака-результата
От ……. до …. От …… до …..
Итого	Общее число элементов совокупности

Дата добавления: 2015-04-24