Дискретные и непрерывные вариационные ряды. Понятие частоты и частости групп. Накопленные частоты (частости) и кумулятивные ряды

Рядами распределения называются числовые ряды, характеризующие структуру совокупности по некоторому признаку. Ряд распределения может быть получен в результате структурной группировки. Ряд распределения, образованный по количественному признаку (вариационный ряд), может быть дискретным (признак принимает ограниченное число возможных значений, например 2,3,4,5) или интервальным (значения признака выражены вещественными числами или число возможных значений признака достаточно велико).

Характеристиками ряда являются:

x_i − варианта (отдельное возможное численное значение признака)

(i=1,k);

n_i − частота (численность отдельных групп);

n − общее число элементов совокупности;

q_i − частость (доля отдельных групп во всей совокупности).

Вариационный ряд оформляется в виде таблицы, где в первой графе указываются варианты (интервалы) значений признака, а в следующих − частота и частость.

Ряд распределения в целом характеризует структуру совокупности по данному признаку. Однако могут использоваться и кумулятивные ряды, т.е. ряды накопленных частот (частостей).

Накопленная частота (частость) − это число (доля) элементов совокупности, у которых значения признака не превышают данного.

Обозначим

F(x) − накопленная частота для данного значения x;

G(x) − накопленная частость для данного значения x.

Эти характеристики обладают следующими свойствами:

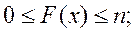
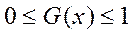
Рассмотрим интервал с номером i: [ x_i 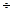x_i+1 ]

Накопленная частота на конец i -го интервала определяется по формуле

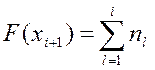
Вариационный ряд можно изобразить в виде графика.

Изображением дискретного ряда является полигон. При его построении по оси абсцисс откладываются варианты (x_i), а по оси ординат − частоты или частости − f_i. Затем точки с координатами (x_i;f_i) последовательно соединяются отрезками прямой.

Изображением интервального ряда является гистограмма. При ее построении по оси абсцисс откладываются интервалы ряда. Над осью абсцисс строится прямоугольник, основанием которого является интервал, а высотой − значение частоты или частости.

Изображением ряда накопленных частот является кумулята. Накопленные частоты откладываются по оси ординат для границ интервалов и соединяются отрезками прямых.

10. Понятие медианы. Вычисление медианы по сгруппированным данным

Медиана представляет собой такое значение признака, которое делит объем совокупности пополам в том смысле, что число элементов совокупности со значениями признака, меньшими медианы, равно числу элементов совокупности со значениями признака, большими медианы.

Численное значение медианы можно определить по ряду накопленных частот. Накопленная частота для медианы равна половине объема совокупности:

.

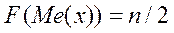Для интервального ряда сначала определяется интервал, в котором будет находиться медиана. Само же значение Ме(x) может быть приближенно определено с помощью интерполяции

,

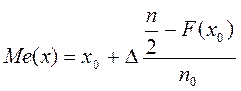где x₀ − начало интервала, содержащего медиану;

 − величина интервала, содержащего медиану;

F(x₀) − накопленная частота на начало интервала, содержащего медиану;

n − объем совокупности;

n₀ − частота интервала, в котором расположена медиана.

12. Показатели вариации. Дисперсия и ее вычисление для не сгруппированных и сгруппированных данных. Среднее квадратичное отклонение и коэффициент вариации

1. Выборочная дисперсия (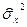) – это среднее значение квадратов отклонений индивидуальных значений признака от средней величины:

- для несгруппированных данных:

,

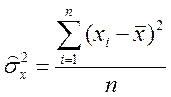- для сгруппированных данных

.

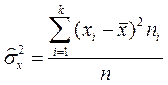Если ряд интервальный, то в качестве x_i берется середина i -го интервала.

Более удобны следующие формулы вычислений:

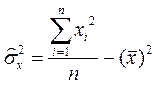
(для несгруппированных данных)

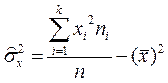
(для сгруппированных данных),

2. Среднее квадратическое отклонение (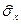) представляет собой квадратный корень из дисперсии

.

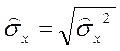Этот показатель является средним квадратическим отклонений значений признака от средней.

3. Коэффициент вариации характеризует относительную величину варьируемости признака в данной совокупности (по отношению к среднему значению)

14. Ряды динамики. Анализ временных рядов. Моментальные и интервальные временные ряды

Временной ряд представляет собой ряд числовых значений какого-либо показателя в последовательные моменты или периоды времени. Числовые значения, составляющие временной ряд, называются уровнями ряда.

По способу построения ряд может быть моментным, когда уровни ряда представлены на определенные моменты времени (конец квартала, начало года и т.д.) и интервальным, когда уровни ряда соответствуют определенным интервалам времени.

Изучение различных процессов на основе временных рядов включает следующие этапы:

- сбор исходной информации и построение временных рядов;

- визуальный анализ временного ряда и формирование набора возможных моделей прогнозирования;

- идентификация (подбор) модели;

- оценка параметров моделей;

- осуществление прогноза по математической модели.

В практике анализа временных рядов принято считать, что значения уровней временных рядов складываются из следующих компонент:

- тренд;

- сезонная составляющая;

- циклическая составляющая;

- случайная составляющая.

Под трендом (тенденцией) понимают изменения, определяющие общее направление развития изучаемого показателя. Это систематическая составляющая долговременного действия. Для описания тренда используют плавно меняющиеся, гладкие функции.

Наряду с долговременными тенденциями во временных рядах часто имеют место более или менее регулярные колебания – периодические составляющие рядов динамики. Если период колебаний не превышает одного года, то их называют сезонными. Причины сезонных колебаний могут быть связаны с природно-климатическими условиями, могут носить социальный характер (например, увеличение покупок в предпраздничные дни, увеличение платежей в конце квартала и т. д.). Для описания сезонной компоненты используют периодические функции.

При большом периоде колебаний считают, что во временных рядах имеется циклическая составляющая. Примерами могут служить демографические, деловые, инвестиционные и другие циклы.

Если из временного ряда удалить тренд и периодические составляющие, то останется нерегулярная компонента. Часто причиной нерегулярных колебаний является действие большого числа различных факторов. Эта компонента рассматривается как случайная.

Моментные ряды отличаются от интервальных принципиальной неполнотой информации.

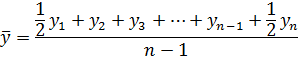
16. Показатели динамики (абсолютный прирост, коэффициент роста, коэффициент прироста) цепные и базисные

Показатели динамики – это величины, характеризующие изменения уровней временного ряда. К ним относятся абсолютный прирост, коэффициент (темп) роста и коэффициент (темп) прироста.

Различают базисные и цепные показатели динамики. Базисные показатели – это результат сравнения текущего уровня ряда с одним фиксированным уровнем, принятым за базу (обычно это начальный уровень ряда). Цепные показатели – это результат сравнения текущего уровня ряда с предшествующим уровнем.

Формулы для расчета показателей представлены в табл.

Таблица

Дата добавления: 2015-04-24