Формы уравнения множественной регрессии

Смысл и значение множественной регрессии в эконометрических исследованиях. Выбор

Свойства остатков

Визуальный анализ остатков

Интервальный прогноз

Определяется средняя ошибка прогнозного индивидуального значения y:

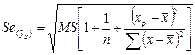
Строится доверительный интервал прогноза:

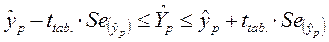
· Отсутствие связи между остатками и объясняющей переменной.

· Отсутствие связи между остатками и предсказанными значениями.

· Математическое ожидание остатков равно нулю. В выборке.

· Остатки имеют постоянную D. D остатков =1. Постоянство D остатков называют гомоскедастичностью остатков. Если же дисперсия остатков непостоянна, то имеет место гетероскедастичность остатков.

· Остатки не коррелированны между собой.

· Остатки распределены по нормальному закону распределения

Осн. цель – построение модели с неск. факторами, определив при этом влияние каждого из них в отдельности совокупности их воздействия на результативные признаки.

М. p. — метод многомерного анализа, посредством к-рого зависимая переменная (или критерий) Y связывается с совокупностью независимых переменных (или предикторов) X посредством линейного уравнения: Y' = а + b1Х1 + b2Х2 +... + bkXk.

1. Получение наилучшего линейного уравнения прогноза.

2. Контроль за смешиванием переменных (факторов).

3. Оценка вклада определенной совокупности переменных.

4. Объяснение сложного на вид многомерного комплекса взаимосвязей.

5. Проведение дисперсионного и ковариационного анализов посредством кодирования уровней независимых переменных.

Наиболее часто используются следующие функции:

линейная ;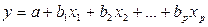

степенная функция ;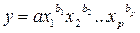

показательная функция ;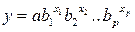

экспонента ;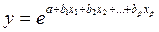

гипербола .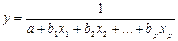

Дата добавления: 2015-04-24