
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Хід уроку. І. Організаційний момент
|
|
|
|
І. Організаційний момент
ІІ. Формулювання мети і завдань уроку.
Слово вчителя.
«В одну ріку не можна увійти двічі» - ці слова приписують давньогрецькому філософу Геракліду Ефеському (з міста Ефес). Вони відображають суттєву особливість реального світу: усе в ньому перебуває у стані безперервної зміни і розвитку. Саме шукаючи закономірності у нескінченному морі видозмін природи, вчені дійшли до понять змінної величини і функції.
Про вагому роль функцій як математичних моделей реальних процесів Ньютон писав так: «Я не зміг би отримати багатьох своїх фундаментальних результатів, якби не відмовився від безпосереднього розгляду самих тіл і не звів усе просто до дослідження функцій».
На уроці ми з вами продовжимо вивчати тему «Функція», зокрема, розкриємо всі секрети лінійної функції і її графіка.
ІІІ. Актуалізація опорних знань.
На домашнє завдання вам було повторити все про функцію, і самостійно опрацювати теоретичний матеріал «Лінійна функція і її графік». Підібрати задачі, які б приводили нас до вивчення лінійної функції:
Інтерактивна гра «Закінчи речення».
1. Змінну у називають функцією від змінної х, якщо кожному значенню....
2. Змінна х —
3. Змінна у —
4. Усі значення, який набуває аргумент, утворюють....
5. Усі значення, яких набуває функція при, аргументах, взятих з області визначення функції, утворюють...
6. Графік функції утворюють точки координатної площини...
7. Функція виду 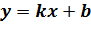 називається...
називається...
8. Пряму пропорційність можна задати формулою...
9. Графіком лінійної функції є пряма...
10.Для того, щоб побудувати графік лінійної функції, достатньо...
11.Якщо точка належить графіку функції, то абсциса цієї точки дорівнює..., а ордината —....
Зачитайте задачі, які приводять нас до поняття лінійної функції.
Задача 1. Одна сторона прямокутника дорівнює х см, а інша — на 4 см більша. Виразити через х периметр Р цього прямокутника.
Р = 4х + 8
Задача 2. Маса одного цвяха 4 г, а маса порожнього ящика 600 г. Виразити залежність між масою ящика із цвяхами т (у г), в якому хцвяхів (де х — натуральне число).
m = 4х + 600.
Задача 3. Зарплата продавця за місяць становить 500 грн. та премія в розмірі 1% від вартості реалізованого товару. Запишіть залежність між зарплатою у (у грн.) і вартістю х (у грн.) реалізованого товару, у = 0,01 х + 500
Задача 4. Мотоцикліст рухається зі швидкістю 65 км/год. Задайте формулою залежність пройденого шляху (у кілометрах) від часу (у годинах).
S = 65t
Запишіть тему уроку: «Лінійна функція, та її графік».
На цьому уроці ми з вами навчимося:
1) розпізнавати лінійні функції та називати їх коефіцієнти;
2) будувати графіки таких функцій та читати їх;
3) за формулою 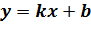 встановлювати властивостіграфіка;
встановлювати властивостіграфіка;
4) за графіком функції запи9увати її формулу.
ІV. Вивчення нового матеріалу. Дослідницька лабораторія.
Завдання 1. № 823 (усно). Чому дорівнює коефіцієнт 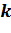 та
та 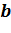 у кожній з цих функцій.
у кожній з цих функцій.
Завдання 2. Кожній групі задана функція. Побудуйте її графік (графік діти будують на окремому аркуші ватмані) і запишіть властивості, відповідаючі на запитання:
1. Знайдіть область визначення даної функції.
2. Знайдіть область значення даної функції.
3. Що є графіком даної функції?
4. Назвати кутовий коефіцієнт даної функції. Який його знак?
5. Який кут нахилу графіка функції з додатнім напрямом осі Ох?
6. Чому дорівнює ордината точки перетину графіка з віссюОy? Порівняйте з коефіцієнтами.
7. Чи проходить графік через початок координат?
Лабораторія 1. 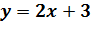
Лабораторія 2. 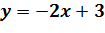
Лабораторія 3. 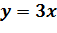 та
та 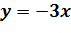
Лабораторія 4. у = 4 та у = 0
По одному представнику з кожної команди виходять до дошки і захищають роботи. Вчитель разом із учнями заповнює узагальнену таблицю.
| Область визначення | Будь-яке число | ||
| Область значень | Будь-яке число | ||
| Графік функції | Пряма | ||
| Кут, який утворює графік функції з додатнім напрямом | 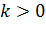
| Гострий | |
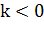
| тупий | ||
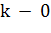
| Пряма паралельна осі Ох | ||
| Ордината точки перетину графіка з віссю Оу | Вказує число 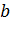 , якщо , якщо 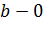 , то графік проходить через початок координат , то графік проходить через початок координат
|
Завдання 3. Побудуйте в одній системі координат графіки функцій. Дайте відповіді на наступні запитання.
1. Що спільного В формулах заданих функцій?
2. Як розміщені графіки заданих функцій один відносно іншого? (Порівняйте кутові коефіцієнти).
3. Коли точка перетину графіків функцій лежить на осі Оу?
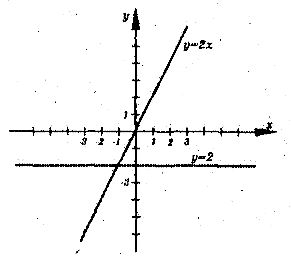 Лабораторія 1. у = 2х та у = -2.
Лабораторія 1. у = 2х та у = -2.
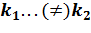
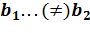
Графіки... (перетинаються)
Лабораторія 2. 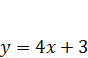 та
та 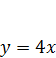 .
.
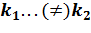
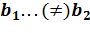
Графіки... ( паралельні)
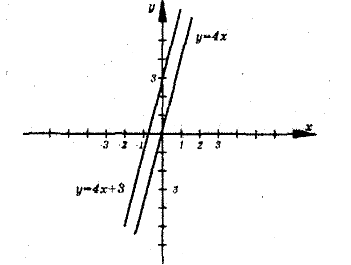
Лабораторія 3. 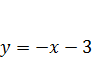 та
та 
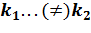
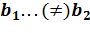
Графіки... ( паралельні)
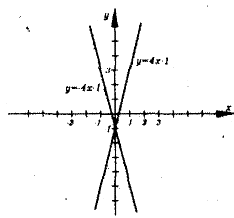 Лабораторія 4.
Лабораторія 4. 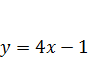 та
та 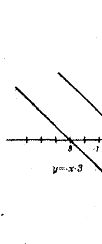 .
.
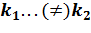
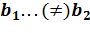
Графіки... ( перетинаються)
Висновки.
1. Якщо коефіцієнти  у функції одинакові, то графіки паралельні, якщо різні, то графіки перетинаються.
у функції одинакові, то графіки паралельні, якщо різні, то графіки перетинаються.
2. Якщо коефіцієнти 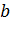 одинакові, то графіки перетинаються на осі Оу.
одинакові, то графіки перетинаються на осі Оу.
Скласти опорну схему: «Залежність між коефіцієнтами k та b і графіком функції у = кх + b (діти складають схеми на окремих аркушах, вчитель коментує кожну з них і узагальнює всі схеми запропонувавши їх об'єднати в одну).
Залежність між розташуванням прямої  та значеннями
та значеннями  i
i 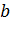
1) 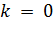 ,
, 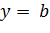 2)
2) 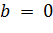 ,
, 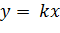 3)
3)  (
(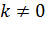 ,
,  )
)
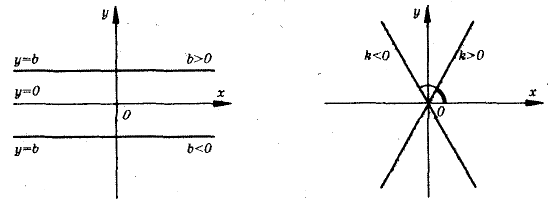
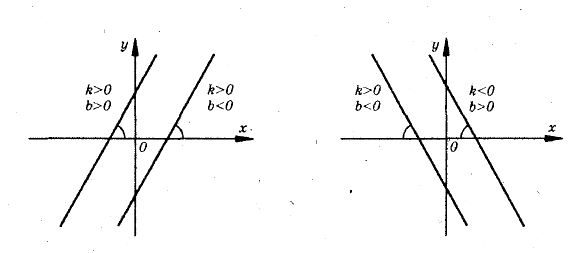
4. Ми з вами навчились маючи формулу лінійної функції, будувати її графік. А зараз навчимось, як за графіком функції записувати її формулу.
Завдання 4. Скласти алгоритм запису формули лінійної функції, яка б відповідала заданому графіку (кожна лабораторія отримує свій графік і записує формулу).
З а п и та н н я -п ід к а з к и
1 Якою формулою задається лінійна функція?
2. Який коефіцієнт ми можемо визначити зразу за графіком?
3. Як знайти інший коефіцієнт(пригадайте, що означає що точка належить графіку функції)?
Алгоритм: (діти записують в зошит).
1. Записуємо загальну формулу лінійної функції.
2. Знаходимо коефіцієнт 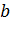 — ордината точки перетину графіка з віссю Оу.
— ордината точки перетину графіка з віссю Оу.
3. Вибираємо будь-яку точку на прямій, знаходимо ко-ординати, складаємо відповідне рівняння, з якого знаходимо коефіцієнт  .
.
4. Записуємо формулу даної лінійної функції.
V. Підсумок уроку.
1. Що нового дізнались? Чому навчились?
2. Що сподобалось?
3. Що викликало найбільші труднощі?.
VI. Домашнє завдання.
П. 25 (означення і Властивості нових понять уроку); № 833, № 837.
Г. П. Стпецик
Проект «Рівняння. Загальні відомості про рівняння»
Тип проекту: інформаційний, короткотривалий.
|
|
|
|
|
Дата добавления: 2015-05-23; Просмотров: 404; Нарушение авторских прав?; Мы поможем в написании вашей работы!