II. Історична довідка (презентація 2 групи)

Перші загальні твердження про тотожні перетворення зустрі­чаються у давньогрецьких математиків, починаючи з VI ст. до н. е. Серед математиків Стародавньої Греції було прийнято вислов­лювати всі алгебраїчні твердження в геометричній формі. Замість додавання чисел говорили про додавання відрізків, добуток двох чисел тлумачили як площу прямокутника, а добуток трьох чи­сел — як об’єм прямокутного паралелепіпеда. Алгебраїчні форму­ли мали вигляд співвідношень між площами і об’ємами. Напри­клад, говорили, що площа квадрата, побудованого на сумі двох відрізків, дорівнює сумі площ квадратів, побудованих на цих від­різках, збільшеною на подвоєну площу прямокутника, побудова­ного на цих відтинка. Таким чином, з’явилися терміни «квадрат числа» (тобто добуток величини на себе), «куб числа», «серед­нє геометричне». Геометричну форму у греків набув і розв’язок квадратного рівняння — вони шукали сторони прямокутника по заданим периметру та площі.

Більшість задач у Греції розв’язувалося шляхом побудов циркулем і лінійкою. Але не всі задачі могли бути розв’язані такими методами. Прикладами таких задач є подвоєння куба, трисекція кута, завдання побудови правильного семикутника.

Всі вони зводились до кубічних рівнянь виду , і 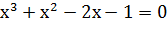відповідно. Для розв’язку цих за­дач було розроблено новий метод, — знаходження точок пе­ретину конічних перетинів (еліпса, параболи і гіперболи).

Окремий значок для, невідомого вперше запровадив давньо­грецький математик Герон у І ст. Але тоді цей предок іксів робив лише перші кроки. Його навіть записували з деякими доповне­ннями, залежно від того, у якому числі і відмінку він стоїть.

Геометричний підхід до алгебраїчних проблем обмежував по­дальший розвиток науки. Наприклад, не можна було додавати величини різних розмірностей (довжина, площа, об’єм), не мож­на було говорити про добуток більш ніж трьох множників тощо. Ідея відмови від геометричного трактування з’явилася у Діофанта Олександрійського, який жив у III ст. У його книзі «Арифмети­ка» з’являється буквена символіка і спеціальні позначення для степенів аж до 6-го. Були у цього і позначення для від’ємних степенів, від’ємних чисел, а також знак рівності (особливого зна­ку для додавання ще не було), стислий запис правил множення додатніх і від’ємних чисел. На подальший розвиток алгебри силь­ний вплив мали досліджені Діофантом задачі, що призводять до складних систем алгебраїчних рівнянь, у тому числі до систем, кількість рівнянь була Меншою кількості невідомих. Для таки рівнянь Діофант шукав лише додатні раціональні розв’язки.

Діофантові рівняння — цоліноміальні рівняння з цілими коефіцієнтами, в яких невідомі змінні можуть приймати тільки ці значення. Названі на честь давньогрецького математика Діофан Олександрійського.

Дата добавления: 2015-05-23