Слово вчителя. На попередніх уроках ми розглянули теореми синусів, косинусів та наслідки з них, ввели поняття розв’язування трикутників

На попередніх уроках ми розглянули теореми синусів, косинусів та наслідки з них, ввели поняття розв’язування трикутників, розглянули основні типи задач на обчислення елементів довільних трикутників. Сьогодні наша мета – узагальнити і систематизувати набуті знання з теми «Розв’ язування трикутників» та показати їх практичне застосування.

III. Мотивація навчальної діяльності

1. Для чого ми вивчаємо тему «Розв’язування трикутників»?

2. Чи потрібні нам ці знання в повсякденному житті? (Обговорення з учнями).

IV. Актуалізація опорних знань.

Перш ніж розпочати роботу, пропоную повторити трохи теорії (метод «Незакінчене речення»).

Замість крапок вставити пропущені слова:

1. У трикутнику проти … лежить більший кут, проти більшого кута лежить... (більшої сторони; більша сторона).

2. Сторони трикутника пропорційні синусам... кутів (протилежних).

3. Кожне з відношень дорівнює ... (діаметру кола, описаного навколо цього трикутника).

4. Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без... (подвоєного добутку цих сторін на косинус кута між ними).

5. Квадрат сторони трикутника дорівнює сумі квадратів двох інших сторін «±» подвоєний добуток однієї з них на проекцію другої. Знак «+» беремо тоді, коли протилежний кут..., а знак «-». коли... (тупий; гострий).

6. Теорему косинусів називають іноді узагальненою теоремою... (Піфагора).

7. Розв’язати трикутник означає: за даними... основними елементами трикутника.... При цьому серед заданих основних елементів хоча б один повинен бути.... (Трьома; знайти три інші його основні елементи; стороною трикутника).

8. Які теореми потрібно знати, щоб розв’язати трикутник? (Теорему синусів, теорему косинусів).

V. Узагальнення та систематизація знань учнів.

Для початку зробимо невеликий екскурс в історію.

Представлення проекту групою «Історики»

Теорема косинусів відома ще стародавнім грекам. У твердженнях 12 і 13 другої книги «Начал» Евкліда розглянуто питання про квадрат сторони трикутника, яка лежить проти гострого і проти тупого кута.

Вчені Індії зводили розв’язування будь-яких трикутників до розв’язування прямокутних трикутників і не потребували теорему синусів і не знали її.

Безпосередньо для плоских трикутників теорему косинусів довів арабський астроном і математик Абу-л-Вафа (940-998). Трохи згодом доводить і використовує цю теорему знаменитий середньоазіатський учений-енциклопедист Ал-Беруні (973-1048).

В Європі теорему косинусів по-справжньому оцінив і почав систематично використовувати знаменитий французький алгебраїст Франсуа Вієт (1540-1603).

Вважають, що теорему синусів вперше довів учитель Ал-Беруні, іранський математик Ібн-Ірак. Доведення цієї теореми зустрічається і в працях Ал-Беруні.

Сучасного виду теорема косинусів набула в 1801 році у французького математика Лазара Карно: теореми косинусів і синусів взаємопов’язані. З кожної з них можна вивести іншу, виконавши відповідні тригонометричні співвідношення.

Ознайомившись з історичною довідкою, дайте відповіді на запитання.

1. В якому столітті видатним астрологом Ал-Беруні була доведена теорема синусів? (У XI).

2. Коли нею почали користуватися європейські математики? (У XVI столітті).

3. Яка теорема була доведена геометрично в «Началах» Евкліда? (Теорема косинусів).

4. Ким і коли вона була сформульована словесно? (Французьким математиком Франсуа Вієтом, XVI століття).

5. Хто і коли надав їй сучасного вигляду? (Французький математик Лазар Карно у 1801 році).

Представлення проекту групою «Теоретики»

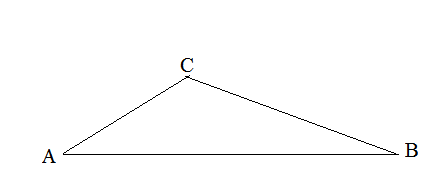
Основні задачі на обчислення елементів довільних трикутників

	Тип задачі	Дано	Знайти	Алгоритм розв'язання
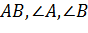
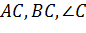
	За стороною і прилег-лими до неї кутами			1. 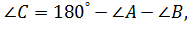2. 3.
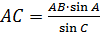
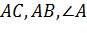
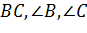
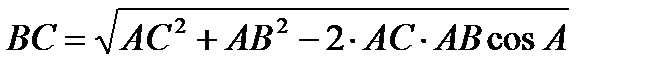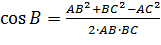	За двома сторонами і кутом між ними			1. 2. 3.
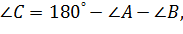
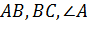
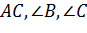
	За двома сторонами і кутом, Протилежним одній із них			1. 2. 3.
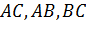
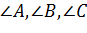
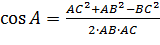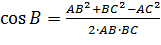	За трьома сторонами			1. 2. 3.

Запитання для групи

1. Що означає розв’язати трикутник?

2. Коли можна отримати два розв’язки?

3. За якими трьома елементами не можна розв’язати трикутник і чому?

VI. Розв’язування задач. Закріплення вмінь та навичок.

Працюючи над проектом, творчо-пошукові групи звертали особливу увагу на задачі, пов’язані з практичним застосуванням.

Представлення проекту групою «Дослідники»

Застосування в геодезії

Є професії, пов’язані з частим розв’язуванням трикутників. Насамперед цим займаються геодезисти. Яке б велике будівництво не розпочиналось, першими туди йдуть геодезисти, щоб зняти план місцевості та охарактеризувати рельєф. Коли ж на основі їх матеріалів у проектних організаціях опрацюють проект, геодезисти знову міряють кути, розв'язують трикутники, забивають кілочки — «прив’язують» опрацьований проект до місцевості.

А навіщо вони розв’язують трикутники? Щоб визначити потрібні відстані, не вимірюючи їх безпосередньо. Є ще спеціалісти, які розв’язують подібні задачі в шахтах, тунелях, метро та інших підземних розробках. Це маркшейдери. їм також часто доводиться розв’язувати трикутники.

Задача 1.

Необхідно побудувати міст через річку з точки А в точку В. Інженер з’ясував, що відстань від точки А до точки С в далину від берега складає 100 м, а в трикутнику АВС кут А дорівнює 96,5°, а кут В дорівнює 46,8°. Якої довжини буде міст?

Задача 2.

Із двох точок А і В, відстань між якими 50 м, вершину гори видно під кутами 50° та 30°. Знайти висоту гори, якщо зріст людини 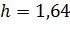м.

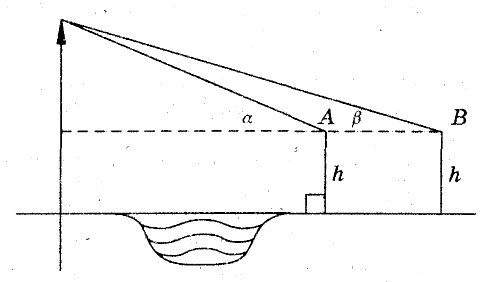
Застосування навігації

Навігація вирішує питання визначення напрямку і пройденої відстані в морі; методи обчислення шляху і способи визначення місця судна в морі за береговими і плавучими орієнтирами за допомогою штурманських приладів; питання керування і безаварійного проведення судна за особливих умов плавання.

Морехідна астрономія вирішує питання визначення місця судна в морі за положенням небесних світил.

Картографія за допомогою теорії картографічних проекцій, що застосовується в судноводінні, розв’язує аналітичним і графічними способами специфічні штурманські задачі з проведення судна з урахуванням дії різних факторів (вітру, течії тощо).

Усі ці науки базуються на чіткій математиці. Але конкретні обставини на йорі, інколи дуже складні, не завжди дозволяють штурману отримати необхідну інформацію з потрібного точністю навіть за допомогою сучасних технічних засобів.

Тому судноводіння, що ґрунтується на науково-математичній основі, гарантує безпеку судна під час плавання в будь-яких умовах.

Уміння здійснити плавання найзручнішим за даних умов шляхом, найбільш точно провести судно в порт призначення, з необхідною точністю визначити місце судна в морі практично на будь-яких відстанях — усе це залежить від судноводія.

І всі задачі розв’язуються із застосуванням знань із тригонометрії.

Задача 3.

Доглядач маяка, перебуваючи на верхньому поверсі маяка, бачить човен, що терпить лихо, під кутом 27,3°. Висота маяка складає 100,2 км. Як далеко від маяка знаходиться човен?

Задача 4.

Корабель С перебуває у 39,9° на північний схід від корабля А і в 15° на північний захід від корабля В, який віддалений від А в східному напрямку на 500 м. На якій відстані один від одного знаходиться А і С?

Задача 5.

Берегові радіомаяки А і В розташовані на відстані 10 км. Із судна С з допомогою радіолокаційної станції, що знаходиться на ній, визначені відстані до маяків 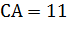км і СВ = 9 км. Знайдіть кути САВ і СВА пеленгів радіомаяків.

Застосування в астрономії

У давнину за допомогою тригонометрії люди навчилися вимірювати уявні трикутники на небі, вершинами яких були зірки. Зараз тригонометрію застосовують навіть для вимірювання відстані між космічними кораблями.

Задача 6.

Астроном вибрав час, коли Планета перебувала з його точки зору на максимальній відстані від Сонця. Вимірювальний кут між Планетою і Сонцем дорівнює 38,5°. Відомо, що Сонце знаходиться на відстані 148800000 км від Землі. Яка відстань від Сонця до Планети?

Задача 7.

Астроном виміряв кут, утворений Сонцем, Землею і Зіркою. Через шість місяців він знову виміряв цей самий кут. Відстань між Сонцем і Землею становить 148800000 км, а виміряні кути відповідно рівні 87,5° і 88°. На якій відстань перебувала Земля і Зірки під час другого вимірювання?

Застосування у військовій справі

Задача 8.

Літак летів 20 хвилин у напрямку 210° (починаючи відлік за годинниковою стрілкою від північного напрямку) зі швидкістю 320 км/год. Потім він змінив курс і протягом 40 хвилин летів у напрямку 265°. На скільки він віддалявся від вихідної точки? Швидкістю вітру можна знехтувати.

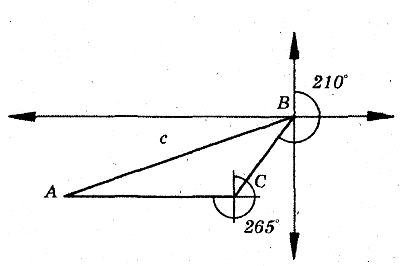
Задача 9.

Радар засік ворожий літак на відстані 42 км і отримав команду його знищити. При розрахунку вийшло, що для потрапляння в літак необхідно запустити ракету під кутом 30°, оскільки за час польоту ракети літак пролетить 24 км. Скільки пролетить ракета до зіткнення з літаком?

Задача 10.

Зі спостережного пункту помічають під кутом 63,5° літак, що пролітає над вежею, висота якої 79,5 м. Пряма, що сполучає спостережний пункт із верхівкою вежі, утворює з горизонтальною площиною кут 20°45'. На якій висоті знаходиться літак?

VII. Підсумок уроку.

1. Закінчити речення:

• Сьогодні на уроці я повторив...

• Сьогодні на уроці я навчився...

• Необхідно додатково попрацювати над...

• Найважчим для мене було...

2. Порівняй свої знання на початку і в кінці уроку і дай відповіді на запитання:

• Чи отримав ти задоволення від власної праці?

• Який етап діяльності був найцікавішим?

• Які загальнонавчальні вміння допомагали у складних ситуаціях?

Учитель. Зробимо підсумок нашої проектної діяльності. Ми побудували проект «Практичне застосування “ Розв’язування трикутників”». У проекті було використано різноманітні задачі практичного змісту. У процесі роботи над проектом ви спостерігали застосування ваших знань для розв’язання проблемі прикладного характеру. Сьогодні ми довели собі, що без математики неможлива успішна діяльність людини.

VIII. Оцінювання учнів.

IX. Домашнє завдання.

1. Металевий прут довжиною 70 см необхідно зігнути під прямим кутом так, щоб відстань між кінцями дорівнювала 50 см. Де повинна знаходитись точка згину?

2. З вертольота, який знаходиться над шосейною дорогою, була помічена колона машин, яка рухалась цією дорогою. Початок колони видно під кутом зниження 75°, а кінець — під кутом 70°. Знайдіть довжину колони, якщо вертоліт знаходиться на висоті 1650 м.

3. Придумати свою задачу практичного змісту на застосування теми «Розв’язування трикутників».

Н. Г. Попович

Проект «Елементи комбінаторики»

Тема проекту: Елементи комбінаторики.

Учасники проекту: учні 11 класу.

Тип проекту: практично-орієнтований.

Термін виконання: 2 тижні.

Епіграф уроку:

«Число, розміщення і комбінацій — три взаємно перетинаючі, але різні сфери думки, якими можна описати всі Математичні ідеї»

(Д. Д. Сильвестр).

I. Актуальність проекту як навчальної технології

Проектне навчання дозволяє розширити коло завдань, які учень розв'язує на уроці, створює умови для творчого розвитку особистості. З’являється елемент зацікавленості у процесі навчання.

II. Мета і завдання проекту

Узагальнити і систематизувати знання з теми: «Елементи комбінаторики», навчити розв’язувати задачі зі сполуками, «здійснювати операції над множинами.

Розвивати творче мислення всебічним аналізом проблем, запам’ятовувати інформацію у вигляді логічних структур, розуміти причинно-наслідкові зв’язки.

III. Механізм реалізації проекту

1. Постановка проблеми.

Починаючи вивчати тему «Елементи комбінаторики», важливо зазначити причину виникнення даного розділу математики і її роль у сучасному суспільстві.

2. Визначення тем і мети проектів.

Для захисту пропонують проекти з таких тем: «Історія виникнення і розвитку науки комбінаторики», «Цікава комбінаторика», «Застосування комбінаторики».

Проекти можна подавати у формі презентацій або рефератів.

3. Захист проектів.

Захист проектів проходить у кінці вивчення теми.

Тип уроку: урок узагальнення і систематизації знань.

4. Оцінювання проектів.

Оцінювання проводить вчитель, враховуючи і якість самих проектів, і відповіді учнів під час уроку.

Дата добавления: 2015-05-23