
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод Хеммінга
|
|
|
|
Ще один важливий метод розв’язування задачі Коші  з початковою умовою y (a) =y 0 на інтервалі [ a, b ] – метод Хеммінга. Прогноз, як і в попередніх методах, базується на наближенні поліномом Лагранжа для f (x, y (x)). Він будується по точках (xi -3, fi -3), (xi -2, fi -2), (xi -1, fi -1) та (xi, fi). При інтегруванні отримаємо прогноз Хеммінга:
з початковою умовою y (a) =y 0 на інтервалі [ a, b ] – метод Хеммінга. Прогноз, як і в попередніх методах, базується на наближенні поліномом Лагранжа для f (x, y (x)). Він будується по точках (xi -3, fi -3), (xi -2, fi -2), (xi -1, fi -1) та (xi, fi). При інтегруванні отримаємо прогноз Хеммінга:

| (19) |
Коректор отримаємо, будуючи ще один поліном Лагранжа для функції f (x, y (x)) по точках (xi -1, fi- 1), (xi, fi) і новій точці (xi +1, fi +1) = (xi +1, f (xi +1, pi +1)). В результаті одержуємо формулу:
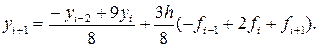
| (20) |
Управляючий параметр:
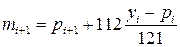 . .
| (21) |
Методи прогнозу-корекції при великому кроці 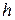 можуть бути нестійкими. В таких умовах похибка збільшується від кроку до кроку, що і обумовлює нестійкість. Для забезпечення стійкості розглянутих методів потрібно корегувати крок на етапі його вибору. Крок вибирається згідно нерівностей:
можуть бути нестійкими. В таких умовах похибка збільшується від кроку до кроку, що і обумовлює нестійкість. Для забезпечення стійкості розглянутих методів потрібно корегувати крок на етапі його вибору. Крок вибирається згідно нерівностей:
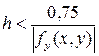
| (в методі Адамса-Бешфорса-Маултона) | (22) |
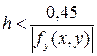
| (в методі Мілна-Сімпсона) | |
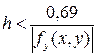
| (в методі Хеммінга) |
Методи Адамса-Бешфорса-Маултона, Мілна-Сімпсона і Хеммінга дозволяють отримати результати з високим рівнем точності за невелику кількість кроків.
|
|
|
|
|
Дата добавления: 2015-05-23; Просмотров: 363; Нарушение авторских прав?; Мы поможем в написании вашей работы!