Определение силы давления покоящейся жидкости на плоские поверхности. Центр давления

Для того, чтобы определить силу давления, будем рассматривать жидкость, которая находится в покое относительно Земли. Если выбрать в жидкости произвольную горизонтальную площадь ω, то, при условии, что на свободную поверхность действует р_атм= р₀, на ω оказывается избыточное давление:

Р_изб = ρghω. (1)

Поскольку в (1) ρgh_ω есть не что иное, как mg, так как h_ω и ρV = m, избыточное давление равно весу жидкости, заключенной в объеме h_ω. Линия действия этой силы проходит по центру площади ω и направлена по нормали к горизонтальной поверхности.

Формула (1) не содержит ни одной величины, которая характеризовала бы форму сосуда. Следовательно, Р_изб не зависит от формы сосуда. Поэтому из формулы (1) следует чрезвычайно важный вывод, так называемый гидравлический парадокс – при разных формах сосудов, если на свободную поверхность оказывается одно и тоже р₀, то при равенстве плотностей ρ, площадей ω и высот h давление, оказываемое на горизонтальное дно, одно и то же.

При наклонности плоскости дна имеет место смачивание поверхности с площадью ω. Поэтому, в отличие от предыдущего случая, когда дно лежало в горизонтальной плоскости, нельзя сказать, что давление постоянно.

Чтобы определить его, разобьем площадь ω на элементарные площади dω, на любую из которых действует давление

По определению силы давления,

причем dP направлено по нормали к площадке ω.

Теперь, если определить суммарную силу которая воздействует на площадь ω, то ее величина:

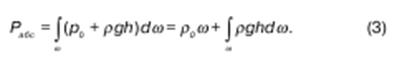
Определив второе слагаемое в (3) найдем Р_абс.

Pабс = ω(p₀ + h_{ц. е}). (4)

Получили искомые выражения для определения давлений, действующих на горизонтальную и наклонную

плоскости: Р_изб и Р_абс.

Рассмотрим еще одну точку С, которая принадлежит площади ω, точнее, точку центра тяжести смоченной площади ω. В этой точке действует сила P₀= ρ₀ω.

Сила действует в любой другой точке, которая не совпадает с точкой С.

Дата добавления: 2015-05-23