Варіанти практичних завдань 2 страница

Література: [1, с. 77 – 99; 4, с. 85 – 102; 7, с. 5 – 33].

Практичні заняття №4-5 (Розв´язання транспортної задачі з економічним аналізом отриманих результатів)

Є три постачальники і чотири споживачі однорідного продукту. Потужності постачальників і попити споживачів, а також витрати на перевезення одиниці вантажу для кожної пари «постачальник-споживач» зведені в таблицю 3 постачань.

Задача полягає у наступному: знайти обсяги перевезень для кожної пари «постачальник-споживач» так, щоб:

1) потужності всіх постачальників були реалізовані;

2) попити всіх споживачів були задоволені;

3) сумарні витрати на перевезення були мінімальні.

Таблиця 3 – Дані для розв’язання транспортної задачі

1 a:={200, 270, 130} b:={120, 80, 240, 160}	16 a:={25, 25, 50} b:={15, 15, 40, 30}
2 a:={110, 190, 90} b:={80, 60, 170, 80}	17 a:={40, 27, 23} b:={30, 25, 15, 20}
3 a:={160, 140, 60} b:={80, 80, 60, 140}	18 a:={15, 58, 35} b:={30, 23, 35, 20}
4 a:={115, 145, 100} b:={70, 220, 40, 30}	19 a:={90, 60, 90} b:={24, 40, 80, 96}
5 a:={180, 100, 120} b:={110, 90, 120, 80}	20 a:={16, 28, 30} b:={22, 18, 13, 21}
6 a:={100, 150, 50} b:={75, 80, 60, 85}	21 a:={30, 25, 50} b:={15, 15, 45, 30}

Продовження таблиці 3

7 a:={45, 85, 20} b:={40, 30, 30, 50}	22 a:={50, 27, 23} b:={35, 30, 15, 20}
8 a:={50, 40, 20} b:={33, 22, 39, 16}	23 a:={25, 58, 35} b:={40, 23, 35, 20}
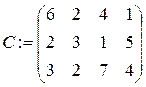
9 a:={35, 85, 60} b:={20, 60, 55, 45}	24 a:={85, 55, 90} b:={24, 40, 80, 86}
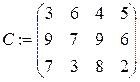
10 a:={16, 24, 30} b:={32, 14, 14, 10}	25 a:={20, 28, 30} b:={22, 18, 17, 21}
11 a:={180, 60, 80} b:={120, 40, 80, 80}	26 a:={100, 270, 130} b:={120, 80, 240, 60}
12 a:={80, 90, 70} b:={80, 50, 70, 40}	27 a:={110, 90, 60} b:={80, 60, 70, 50}

Продовження таблиці 3

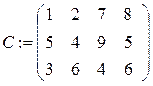
13 a:={75, 200, 220} b:={180, 120, 90, 105}	28 a:={150, 140, 60} b:={70, 80, 60, 140}
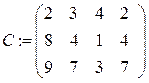
14 a:={130, 80, 160} b:={70, 60, 120, 120}	29 a:={65, 85, 30} b:={50, 40, 30, 60}
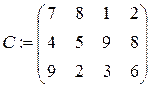
15 a:={160, 140, 170} b:={120, 50, 190, 110}	30 a:={180, 200, 20} b:={110, 90, 120, 80}

Література: [1, с. 102 – 138; 4, с. 117 – 139; 8, с. 5 – 35].

Практичне заняття №6 (Розв´язання задачі про призначення)

У конструкторському бюро потрібно розробити проект машини, що складається з п´яти вузлів. До їх розробки можна залучити п´ять конструкторів. Відомий час, що витрачається кожним конструктором на розробку будь-якого вузла, (див. таблицю 4). Потрібно визначити, хто і який вузол машини повинен проектувати, щоб сумарний час проектування всієї машини був мінімальним.

Таблиця 4 – Дані для розв’язання задачі про призначення

1

16

Продовження таблиці 4

2	17
3	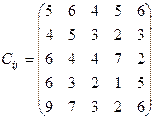18
4	19
5	20
6	21
7	22

Продовження таблиці 4

	23
9	24
10	25
11	26
12	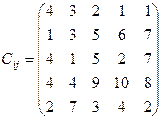27
13	28

Продовження таблиці 4

14	29
15	30

Література: [1, с. 143 – 156; 4, с. 146 – 171; 8, с. 5 – 35].

Практичні заняття № 7 (Розв´язання задачі цілочислового рограмування)

= · Х

А·х= ,

Х 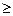0, цілочисловий.

Матриця системи обмежень А, права частина системи обмежень, вектор , вектор з функції мети z для кожного варіанта завдань надані в таблиці 5.

Таблиця 5– Дані для розв’язання задачі цілочислового програмування

№ вар.	Z	Матриця А		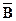№ вар.	Z	Матриця А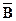
	min		-1	-2			-3		min			-1
			-2	-3	-1		-8				-2	-3	-1		-8
			-3	-6					-1	-4	-6
	max								min		-1	-2			-1
			-1					-1
				-1						-1	-2
	max				-1				max			-1

Продовження таблиці 5

		-1			-2		-2
	max		-3	-4	-2		-13		min	-2		-1	-1		-7
		-1							-1
				-1						-4	-1	-1	-1
	max		-2	-1			-1		min
							-1	-4
				-2							-1
	min		-2	-3	-1		-5		min
		-1
		-1	-5	-5				-3	-6	-3
	min			-1					min		-2	-1			-1
	-1	-2			-3				-2
			-1					-1	-4	-1
	max								max			-1
		-1					-3	-4	-2		-9
			-2
	max			-1					min		-2	-3	-1		-7
								-1
		-2							-1	-5	-3
	min								max			-1			-1
			-1	-4									-1
				-1							-1
	max			-1					min
	-3	-4	-2		-11				-2
								-3	-6	-3
	min	-2		-1	-1		-7		min		-1	-4

Продовження таблиці 5

		-3	-4	-2									-1
	min		-2	-3	-1		-4		max
	-1	-2			-1			-1
				-2	-5						-2
	max		-3	-4	-2		-7		max				-1
		-1							-2
											-2
	min			-1					min			-1
	-2	-3	-1		-8		-1	-2			-1
		-1	-7	-5						-3

Література: [1, с. 163 – 187; 4, с. 175 – 193; 8, с. 28 – 35].

Практичні заняття № 8 (Розв´язання задач динамичного програмування)

Задача 1 (Про розподіл капіталовкладень між чотирма підприємствами)

Постановка задачі. Знайти оптимальний план розподілу капіталовкладень S= 25 грош.од. між чотирма підприємствами, якщо приріст випуску продукції для i - го підприємства, r_i(x), і=1,…,4, залежно від обсягу капіталовкладень, x, відомий і заданий у таблиці 6, де n₁ –перша, а n₂ –друга цифри номера студента у списку групи, [n₂/5] – ціла частина числа n₂/5.

Задача 2 (Про заміну устаткування без урахування його залишкової вартості)

Таблиця 6– Обсяг капіталовкладень і приріст випуску продукції для підприємств

Обсяг кап. вкладень X	r1(x)	r2(x)	r3(x)	r4(x)
	18+n1	20+[n2/5]	16+[n2/4]	20+[n2/5]
	20+n1	21+[n2/2]	27+[n2/5]	23+n1

Продовження таблиці 6

	27+n1	31+[n2/3]	34+[n2/3]	26+n1
	31+n1	37+[n2/3]	40+[n2/4]	31+[n2/3]
	40+n1	40+[n2/2]	41+[n2/2]	40-n1

Постановка задачі. Нехай r(t) – вартість продукції, виробленої за рік на одиниці устаткування, вік якого t років; L(t) – щорічні витрати на обслуговування цього устаткування; S(t)=0 – залишкова вартість устаткування; Р – вартість нового обладнання. Уведемо функцію φ(t)=R(t)-L(t) – різниця між вартістю виготовленої продукції та експлуатаційними витратами. Значення функціі φ(t) за роками наведені у таблиці 7. Нехай Р=10+[n₂/2], де n₂ –друга цифра номера студента у списку групи, [n₂/2] – ціла частина числа n₂/2.

Таблиця 7– Значення функції φ(t) за роками

t
φ(t)

Визначити оптимальний цикл заміни устаткування за період часу тривалістю шість років, причому за ці роки прибуток f₆(t), повинен бути максимальним.

Практичні заняття № 9 (Розв´язання задачі стохастичного програмування)

Постановка задачі. Нехай є два родовища А та В корисної копалини, запаси якої відповідно дорівнюють х та у од. Для видобутку копалини використовується одна машина, що або з визначеною можливістю добуває частину золота, або виходить із ладу і надалі не використовується. Якщо машина працює на родовищі А, то з можливістю Р₁ вона добуває частину r₁, наявного запасу і з можливістю 1-Р₁ виходить із ладу. Якщо на родовищі В, то відповідні дані Р₂; r₂; 1-P₂.

У якій послідовності варто використовувати машину на родовищах на протязі трьох років, щоб загальна кількість корисної копалини, добутої до виходу машини з ладу, була максимальною при заданих х = 400 - 10n₂; у=200+10n₂; р₁ = 0,6+n₁/10; r₁ = 0,8-n₁/10; p₂ = 0,8-n₁/10; r₂ = 0,6+n₁/10, де n₁ –перша, а n₂ –друга цифри номера студента у списку групи.?

3 ТИПОВИЙ РОЗВ΄ЯЗОК ЗАДАЧ

Завдання 1 Дана З Л П:

minZ=3X₁-X₃+X₄-2X₅

X₁-X₂+2X₃+4X₄=11

X₁-X₂+3X₃+6X₄+X₅=19

-2X₁+3X₂-5X₃-11X₄=-26

.

1.Методом Жордана-Гауса:

а) знайти початковий опорний план і обчислити Z();

б) перейти до іншого опорного плану і обчислити Z().

2. Для одного з опорних планів виразити базисні змінні через вільні, перейти від рівностей в обмеженнях задачі до нерівностей і розв’язати задачу геометрично.

3. Виходячи з опорного плану з «гіршою» функцією мети, замінити задачу лінійного програмування в канонічній формі та розв’язати її симплекс-методом.

4. Розв’язати вихідну задачу методом штучного базису.

Дата добавления: 2015-05-23