Розв’язок. 1.а) усі обчислення за методом Жордана-Гауса будемо робити в таблиці 6, попередньо помноживши третє рівняння на -1

1.а) усі обчислення за методом Жордана-Гауса будемо робити в таблиці 6, попередньо помноживши третє рівняння на -1, щоб b₃=26>0. Позначимо .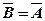

Таблиця 8 − Обчислення за методом Жордана-Гауса

№ кроку	Ā1	Ā2	Ā3	Ā4	Ā5	Ā0
		-1
		-1
		-3
		-1
		-1

Продовження таблиці 8

				-2
				-1
		-1
				-2
	-1

Обравши a₁₁=1 розв´язувальним елементом, застосуємо формулу прямокутника і перерахуємо елементи нової таблиці на 1-му кроці. При виборі розв´язувального елемента враховуємо дві умови: компоненти A₀ у новій таблиці повинні бути не менше нуля і для спрощення рахунку розв´язувальний елемент повинен бути ближчим до 1, а найкраще – дорівнювати 1. Тому після

1-го кроку для перерахування таблиці розв´язувальний елемент a₃₃=1, тому що в 1 і 2-ому рівняннях уже є базисні змінні X₁ й X₅ (вектори Ā₁ і Ā₅одиничні). У результаті 2-го кроку були отримані три базисні змінні X₁, X₅ і X₃, яким відповідають базисні одиничні вектори Ā₁, Ā₅, Ā₃. Узявши вільні змінні X₂ = X₄ =0, одержимо початковий опорний план З Л П 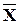*=(3;0;4;0;4), якому відповідає функція мети Z₁=3·3-4·1-2·4=-3.

1.б) перейдемо на 3-му кроці до іншого опорного плану. Для цього треба замість якої-небудь базисної змінної ввести іншу. Наприклад, замість X₁ X₂. При цьому розв´язувальний елемент a₁₂=1 і усі компоненти A₀ у новій таблиці > 0. У результаті перерахування таблиці одержали після 3-го кроку нові базисні змінні X₂, X₅, X₃(базисні одиничні вектори Ā₂, Ā₅, Ā₃) і новий опорний план 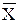_on =(0;3;7;0;1), що забезпечує функцію мети Z₂=0·3+3·0-7·1+0-2·1= -9.

2. Розв´яжемо задачу геометрично. Це можливо, тому що n – m = 5 – 3 = 2.

З огляду на результати, отримані на 3-му кроці, з таблиці 6 маємо систему рівнянь

X₁+X₂ -2X₄ =3; X₂=3-X₁+2X₄≥0

-X₁ +X₄+X₅=1; => X₅=1+X₁-X₄≥0

X₁ +X₃+ X₄ =7; X₃=7-X₁-X₄≥0

X_i≥0, і=1,…,5.

Виразимо Z через X₁ і X₄, з огляду на отримані вирази базисних змінних X₂, X₅, X₃ через вільні X₁ і X₄

Z=3X₁-(7-X₁-X₄)+X₄-2(1+X₁-X₄)=-9+2X₁+4X₄ .

Тоді розв'язувана З Л П має вигляд:

min Z=-9+2X₁+4X₄; -9+ minZ₁=2X₁+4X₄

X₁-2X₄≤3

-X₁+X₄≤1 X₁≥0

X₁+X₄≤7 X₄≥0.

Побудуємо багатогранник розв'язків на площині X₁OX₄ у 1-й чверті.

Граничні прямі: будуємо за двома точками

X1
X4	-1,5

X₁-2X₄≤3: => X₄ ³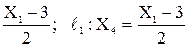

X1		-1
X4

X₄≤1+X₁ => ℓ₂: X₄=7-X₁;

X1
X4

X₄≤7+X₁ => ℓ₃: X₄=7-X₁;

Шукані напівплощини позначимо штрихами. У результаті перетину напівплощин одержуємо багатокутник розв'язків ОАВСД, (рис.1).

Рис.1 Графічне розв΄язання З Л П

Для відшукування min Z₁ будуємо нормальний вектор N = (2;4) і сім´ю рівнобіжних прямих, що задаються Z₁, перпендикулярних N.

Як випливає з рис.1, min Z₁ = Z₁ (0) = Z₁ (0;0) = 2·0+4·0 = 0, то min Z = Z(0) = -9. Для відшукування оптимального плану вихідної задачі підставимо знайдені оптимальні X°₁=X°₄=0 до (1). Одержимо X°₁=0; X°₂=3; X°₃=7; X°₄=0; X°₅=1.

3. Розв´яжемо симплекс-методом задачу, розглянуту в попередньому прикладі. За початковий опорний план візьмемо перший опорний план 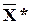=(3;0;4;0;4), якому відповідає функція мети Z₁=-3 зі значенням, більшим, ніж для другого опорного плану 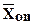(Z₂=-9). Це дозволить зробити симплексним методом, принаймні, одне перерахування таблиці, тому що 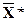неоптимальний.

У цьому випадку ЗЛП має канонічну форму вигляду:

X₁+X₂-2X₄ =3

X₂-X₄+X₅ =4

-X₂+X₃+3X₄=4

X_j≥0, (j=1,..,5).

min Z=3X₁-X₃+X₄-2X₅

Розв´яжемо цю задачу за алгоритмом симплекс-методу. Для цього заповнимо симплекс-таблицю, таблиця

Таблиця 9 – Симплекс - таблиця

Баз.	С	Xбаз			-1		-2	Θ0
змін.	базис.		X1	X2	X3	X4	X5
X1						-2		3/4
X5	-2					-1		4/1
X3	-1			-1				-
Z	=	-3				-8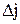
X2						-2
X5	-2		-1
X3	-1
Z=-9	-2			-4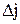

Обчислюємо 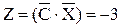й оцінки 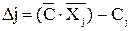. Оскільки ∆₂=2>0,то план 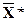не оптимальний. Тому шукаємо інший опорний план, уводячи змінну X₂, вектор Ā₂, у базис. Для перерахування таблиці знаходимо симплексне відношення для X₂ Θ₀ = min(3/1; 4/1)=3. Тоді X₁₂=1 є розв´язувальним елементом. За формулої прямокутника перераховуємо всю таблицю, у тому числі й елементи останнього оцінного рядка. Оскільки всі 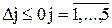, то отриманий опорний план 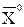=(X₁=0; X₂=3; X₃=7; X₄=0; X₅=1) оптимальний, причому функція мети Z(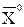)=-9.

Зауваження 1. Для простоти перерахування таблиці використовувалась така схема (правило або формула прямокутника (23)), рис.2:

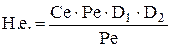, (23)

Рис.2 – Схема правила прямокутника

де Н.е –елемент у новій таблиці, що займає ту саму позицію, що і С_е –елемент у старій таблиці; P_е– розв´язувальний елемент; D₁ і D₂ –додаткові елементи, що стоять на другій діагоналі прямокутника, якщо вважати, що першу діагональ складають елементи С_е і Р_е.

Зауваження 2. Правило заповнення оцінного рядка для початкової симплекс-таблиці можна для наступних симплекс-таблиць застосовувати з метою перевірки правильності обчислень за формулою прямокутника.

4. Розглянемо і розв´яжемо З Л П методом штучного базису, наведену в прикладі.

Складемо з вихідної задачі М – задачу. У 2-му рівнянні є базисна змінна X₅, тому туди не додаємо штучну змінну.

minZ=3X₁-X₃+X₄-2X₅+M(X₆+X₇)

X₁-X₂+2X₃+4X₄+X₆=11

X₁-X₂+3X₃+6X₄+X₅=19

2X₁-3X₂+5X₃+11X₄+X₇=26

Xj≥0, .

Запишемо дані в симплекс-таблицю, таблиця 10, і заповнимо оцінні рядки 4 і 5 за формулами (24)

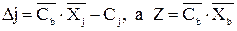. (24) Таблиця 10 – Симплекс-таблиця М­– задачі

					-1		-2	М	М
Xb	Cb	(Xb)i	X1	X2	X3	X4	X5	X6	X7	Θ
X6	M			-1						11/4
X5	-2			-1						19/6
X7	M			-3						26/11
БезM	Z	-38	-5		-5	-13				∆'j
СМ	Z			-4						∆''j
Х6	M	17/11	3/11	1/11	2/11				-4/11	17/3
X5	-2	53/11	-1/11	7/11	3/11				-6/11
X4		26/11	2/11	-3/11	5/11				1/11	26/2
БезM	Z	80/11	-29/11	-17/11	10/11				13/11	∆'j
CM	Z	17/11	3/11	1/11	2/11				-15/11	∆''j
X1		17/3		1/3	2/3			11/3	-4/3	17/2
X5	-2	16/3		2/3	1/3			1/3	-2/3
X4		4/3		-1/3	1/3			-2/3	-1/3
БезM	Z=	23/2		-2/3	8/3			29/3	7/3	∆'j
CM	Z=0									∆''j
X1						-2				3/1
X5	-2					-1				4/1
X3	-1			-1						-
Z	=	-3				-8				∆j
X2						-2
X5	-2		-1
X3
Z		-9	-2			-4				∆j

У 5-му (m+2) рядку є оцінки ∆ ''_j >0 (∆₁=3;∆₃=7;∆₅=15)

Тому опорний план М-задачі не оптимальний. Оскільки ∆₅=15 (оцінка з М) найбільша, то X₄ введемо в базис. Знайдемо для X₄ симплексне відношення Θ₀=min(11/4;19/6;26/11)=26/11.

Тому розв´язувальний елемент дорівнює 11 і X₇ виводимо з базису. Для цього перераховуємо таблицю, застосовуючи симплексний алгоритм, і так далі.

Після двох перерахувань таблиці або двох ітерацій у базисі не залишиться штучних змінних, базисні змінні X₁,X₄,X₅, m+2 (п'ятий) рядок відкидаємо й аналіз проводимо за четвертим рядком. Оскільки ∆₃=8/3>0, то отриманий опорний план не оптимальний і в базис уводимо змінну X₃ (вектор А₃) замість X₄, Θ₀=min(17/2;16;4)=4.

Розв´язувальний елемент дорівнює 1/3. Після перерахування таблиці одержуємо, що опорний план з базисними змінними не оптимальний, тому що ∆₂=2>0. Тому X₂ вводимо як нову базисну змінну замість X₁, бо Θ₀=min(3/1;4/1)=3.

У результаті перерахування симплекс–таблиці одержали оптимальний план 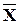⁰=(X⁰₁=0; X⁰₂=3; X⁰₃=7; X⁰₄=0; X⁰₅=1), тому що всі ∆j≤0, що забезпечує

min Z=Z(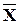 ⁰)= –9.

Завдання 2 Задача про розподіл ресурсів

Підприємство може виготовляти чотири види продукції П-1, П-2, П-3, П-4. Збут будь-якого її обсягу забезпечений. Норми витрати ресурсів і прибуток від одиниці кожного виду продукції надані в таблиці 11. Виконати економічний аналіз лінійної моделі:

1) побудувати модель вихідної та двоїстої задач, знайти оптимальні плани x⁰ і y⁰;

2) дати економічне тлумачення основних і додаткових змінних вихідної та двоїстої задач;

3) проаналізувати доцільне розширення асортименту продукції за рахунок включення нової продукції П₅;

4) установити діапазони зміни вихідних даних за ресурсами і ціною од. продукції, за яких структура оптимального плану не змінюється

Таблиця 11– Дані задачі розподілу ресурсів

Обсяг ресурсів: трудових, матеріальних, верстатних	Норми витрат ресурсів на од. продукції	Нова продукція
П-1	П-2	П-3	П-4	П-5
Ціна од. продукції

Дата добавления: 2015-05-23